Методика построения логарифмических частотных характеристик разомкнутой САУ.

Как было показано ранее, любую многоконтурную разомкнутую си­стему управления методами структурных преобразований можно привести к одноконтурной системе, передаточная функция которой будет равна произведению передаточных функций звеньев одноконтурной цепи [1,2]:

W(p)=W₁(p)·W₂(p),…,W_n(p). (11.1)

Тогда амплитудно-фазовая характеристика этой системы опреде­лится при подстановке ρ=jω в выражение (11.1):

W(jω)= W₁(jω)· W₂(jω),…, W_n(jω). (11.2)

Следовательно, амплитудно-фазовая характеристика системы будет равна произведению амплитудно-фазовых характеристик звеньев ее од­ноконтурной цепи.

Представим выражение для амплитудно-фазовых характеристик в следующем виде:

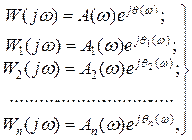(11.3)

где А_i(ω) – амплитудно-частотная характеристика;

θ_i(ω) - фазо-частотная характеристика.

После подстановки выражений (11.3) в выражение (11.2) полу­чим:

А(ω)= А₁(ω)· А₂(ω),…, А_n(ω);

θ(ω)= θ ₁(ω)+ θ ₂(ω)+…+ θ _n(ω); (11.4)

Из выражения (11.4) видно, что амплитудно-частотная характе­ристикаА(ω) разомкнутой системы равна произведению амплитудно-частотных характеристик составляющих звеньев, а фазо-частотная ха­рактеристика равна сумме фазо-частотных характеристик звеньев од­ноконтурной САУ.

Ясно, что при графических построениях фазо-частотную харак­теристику системы θ(ω) можно достаточно легко получить простым суммированием фазо-частотных характеристик отдельных звеньев. Для получения же амплитудно-частотной характеристики А(ω)САУ необхо­димо производить операцию перемножения амплитудно-частотных харак­теристик отдельных звеньев, что при графических построениях крайне неудобно. Кроме этого, часто при построении амплитудно-фазовых ха­рактеристик оказывается, что модули векторов этих характеристик из­меняются в очень широких пределах при изменении ω, что затрудняет их графическое изображение.

Применение логарифмического масштаба значительно упрощает по­строение кривых частотных характеристик, так как в логарифмичес­ком масштабе кривые очень близки к своим асимптотам.

Вследствие этого довольно широкое распространение для иссле­дования систем автоматического управления получили логарифмические частотные характеристики.

Логарифмическая амплитудно-частотная характеристика обычно обозначается L(ω) и равна:

L(ω)=20lg·А(w), (11.5)

т.е. при построении графика L(ω) на оси ординат откладывают не А(w), а двадцать десятичных логарифмов А(w) и измеряют ее в децибелах. По оси абсцисс частота w откладывается в логарифми­ческом масштабе (lg w). За единицу измерения по оси частот при­нимают декаду, которая представляет собой отрезок на оси абсцисс, соответствующий десятикратному изменению частоты. Логарифмическую фазо-частотную характеристику будем обозначать через φ(w), при этом ее значения по оси ординат откладывают в градусах, а масштаб по оси частот тотже, что и при построении L(ω).

На основании выражений (11.4) и (11.5) логарифмические частот­ные характеристики системы будут равны:

(11.6)

Следовательно, логарифмические частотные характеристики си­стемы находятся простым суммированием логарифмических частотных характеристик звеньев одноконтурной цепи.

Рассмотрим методику построения приближенной логарифмической амплитудно-частотной характеристики разомкнутой системы по извест­ной передаточной функции разомкнутой системы. При этом под прибли­женной амплитудно-частотной характеристикой будем понимать характе­ристику, составленную из асимптот точной характеристики.

Для общности рассмотрения будем считать, что одноконтурная цепь исследуемой системы содержит все шесть наиболее распространен­ных типовых звеньев, соединенных последовательно.

Передаточная функция САУ имеет вид:

W(p)=W₁(p)·W₂(p) ·W₃(p) ·W₄(p) ·W₅(p) ·W₆(p),

а передаточные функции звеньев равны:

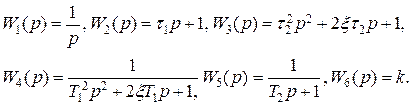
Для определенности исследования примем следующие значения па­раметров передаточных функций:

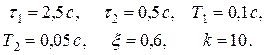
Строим приближенные логарифмические амплитудно-частотные ха­рактеристики звеньев на одном графике (рис. 11.1). Для этого пред­варительно определяем сопрягающие частоты характеристик звеньев:

- для форсирующего звена I порядка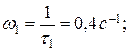

- для форсирующего звена II порядка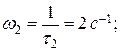

- для колебательного звена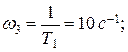

- для апериодического звена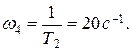

Рис.11.1. К методу построения ЛЧХ

Вполне очевидно, что построенные характеристики усилительно­го звенаW₆(p) и интегрирующего звена W₁(p) будут являться точ­ными характеристиками.

На основании выражения (11.6) для получении логарифмической амплитудно-частотной характеристики системы производим алгебраическое суммирование ординат характеристик звеньев. При этом для про­стоты построения не будем вначале учитывать характеристику усилитель­ного звена.

Начальный участок характеристики системы (до первой сопря­гающей частоты) определяется характеристикой интегрирующего звена и представляет собой отрезок прямой с наклоном - 20 дБ/дек. При со­прягающей частоте w₁= 0,4 с^-1, соответствующей форсирующему зве­ну первого порядка, характеристика системы делает излом на +20 дБ/дек и будет представлять собой до следующей сопрягающей частоты отре­зок прямой, параллельный оси частот.

При сопрягающей частоте w₂= 2 с^-1, соответствующей форси­рующему звену второго порядка, характеристика системы делает излом на + 40 дБ/дек и представляет собой до следующей сопрягающей ча­стоты отрезок прямой с наклоном + 40 дБ/дек. При сопрягающей часто­те w₅= 10 с^-1, соответствующей колебательному звену, она делает излом на - 40 дБ/дек и представляет собой до следующей сопрягаю­щей частоты отрезок прямой, параллельной оси частот. При сопрягаю­щей частоте w₄= 20 с^-1, соответствующей апериодическому звену, характеристика системы делает излом на - 20 дБ/дек и будет представ­лять собой отрезок прямой с наклоном - 20 дБ/дек.

При этих построенияхмы не учитывали характеристику усилитель­ного звена. Вполне очевидно, что для учета этой характеристики не­обходимо сдвинуть полученную характеристику системы параллельно са­мой себе на величину 20lgk=20 дБ.

Приведенные построения и полученные результаты показывают, что приближенная логарифмическая амплитудно-частотная характеристи­ка системы может быть получена и без построения характеристик от­дельных звеньев, а сразу по виду передаточной функции системы.

Для этого необходимо, во-первых, определить сопрягающие ча­стоты звеньев системы, знаяих постоянные времени, и отметить эти частоты на оси частот. Затем следует построить низкочастотную часть характеристики системы, т.е. участок характеристики до первой со­прягающей частоты. Эта часть характеристики будет представлять со­бой отрезок прямой с наклоном -20n дБ/дек, где n - порядок астатизма САУ. При этом ее строить необходимо так, чтобы при частоте w= 1 с^-1 ордината характеристики имела значение, равное 20 lg k,где k - передаточный коэффициент системы.

Такой вид низкочастотной части характеристики системы вытека­етиз того, что приближенные логарифмические амплитудно-частотные характеристики остальных звеньев до первой сопрягающей частоты имеют нулевой наклон.

После этого по виду передаточной функции системы строим дру­гие участки характеристики системы. При этом после каждой из сопрягающих частот изменяем наклон характеристики L(w) по сравнению с тем наклоном, который она имела до рассматриваемой сопрягающей ча­стоты, в зависимости от того, какому звену сопрягающая частота со­ответствует. Если сопрягающая частота соответствует апериодическому звену, то наклон изменится на - 20 дБ/дек, если колебательному звену, то на - 40 дБ/дек, если форсирующему звену второго порядка, то на + 40 дБ/дек.

Затем необходимо уточнить вид полученной приближенной харак­теристики системы, для чего необходимо воспользоваться соответствую­щими таблицами или кривыми поправок. Можно еще уточнить вид получен­ной характеристики и путем непосредственного подсчета точных значе­ний L_i(w) в точках излома, а затем полученные точки соединить отрезками прямых.

Очень часто приближенные логарифмические амплитудно-частот­ные характеристики называются асимптотическими.

Фазовая характеристика системы находится путем простого сум­мирования фазовых характеристик отдельных звеньев. Следует заметить, что построение фазовых характеристик апериодического звена и форси­рующего звена первого порядка, колебательного звена и форсирующего звена второго порядка значительно упрощается за счет применения со­ответствующих шаблонов.

Мы рассмотрели случай построения L(w), когда передаточная функция системы была представлена в виде произведения простейших сомножителей, являющихся передаточными функциями типовые звеньев.

Очень часто, особенно после свертывания многоконтурных схем САУ, передаточная функция системы не представляет собой произведе­ния простейших сомножителей. Тогда, если можно, надо представить многочлены числителя и знаменателя передаточной функции в виде про­изведения простейших сомножителей и производить построение L(w) описанный выше способом. Если это сделать затруднительно, то по­строение L(w) и φ(w) необходимо производить путемих вычисления при различных частотах, лежащих в пределах от 0 до ∞.

2. Анализ устойчивости САУ с использованием логарифмических частотных характеристик.

Широкое применение в инженерной практике получил метод иссле­дования устойчивости САУ с использованием логарифмических частотных характеристик (ЛЧХ). Это объясняется тем, что построение ЛЧХ ра­зомкнутой САУ значительно проще, чем построение кривой Михайлова или АФХ разомкнутой САУ (РСАУ).

Определим требования, которым должны удовлетворять ЛЧХ РСАУ, чтобы замкнутая САУ (ЗСАУ) была устойчивой, используя амплитудно-фазовый критерий устойчивости Найквиста [II].

Устойчивость замкнутой САУ свя­зана с разностью между числом положительных и отрицательных пере­ходов АФХ W(jw)РСАУ через отрезок (-∞, -1) отрицательной вещест­венной оси, т.е. когда А(w)=|W(jw)|>1, а ординаты логарифми­ческой амплитудной частотной характеристики (ЛАЧХ) положительны L(w)> 0. При этом, когда АФХ W(jw) разомкнутой САУ пересекает отрезок (-∞, -1) вещественной оси (рис. 11.2), логарифмическая фазо-частотная характеристика (ЛФЧХ) пересекает одну из линий ±π(2i+1), где i = 0, 1, 2, ...

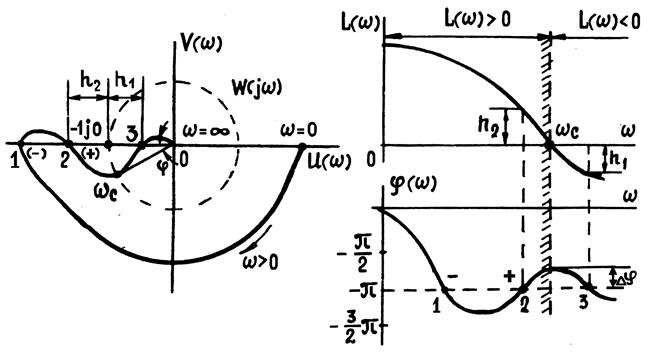
Рис.2.18. К определению устойчивости САУ по ЛЧХ

Переходы АФХ РСАУ через отрезок (-1, 0) вещественной оси А(w)=|W(jw)|<1, когда ординаты ЛАЧХ отрицательны L(w)<0, не учи­тываются при анализе устойчивости САУ. Поэтому область отрицатель­ных значений ЛАЧХ при оценке устойчивости САУ не рассматривается.

Известно (рис. 11.2), что положительному переходу (сверху вниз) АФХ через отрезок (-∞, -1) отрицательной вещественной оси соответствует пересечение ЛФЧХ при L(w)> 0 прямых ±π(2i+1) снизу вверх (точка 2 на рис. 11.2), а отрицательному переходу – сверху вниз (точка 1 на рис.11.2).

Таким образом, критерий устойчивости Найквиста на основе ло­гарифмических частотных характеристик может быть сформулирован сле­дующим образом [II]: для того чтобы замкнутая САУ была устойчива. необходимо и достаточно, чтобы разноса между числом положительных и отрицательных переходов логарифмической фазо-частотной характе­ристикой РСАУ линии ±π(2i+1), (i=0, 1, 2,…) во всех обла­стях, где логарифмическая амплитудно-частотная характеристика РСАУ положительна L(w)> 0, была равна l/2. где l- число правых корней характеристического уравнения разомкнутой системы.

На рис. 11.2 изображены АФХ устойчивой разомкнутой САУ (l=0) и соответствующие ей ЛАЧХ и ЛФЧХ. Таккак разность между числом положительных и отрицательных переходов ЛФЧХ прямой -π при L(w)> 0 равна нулю и l=0, то САУ устойчива в замкнутом состоянии. Запасы устойчивости по амплитуде равны h₁ и h₂, а запас устойчивости по фазе равенΔφ.