Оценка точности САУ в установившемся режиме
Одним из показателей качества регулирования является точность работы системы в установившемся режиме. Оценка точности работы системы может проводиться как по выходной координате 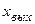 , так и по величине ошибки e. Обычно такая оценка дается по величине установившейся ошибки
, так и по величине ошибки e. Обычно такая оценка дается по величине установившейся ошибки 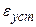 .
.
Установившееся значение ошибки 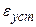 может быть определено на основании предельного свойства преобразования Лапласа следующим образом:
может быть определено на основании предельного свойства преобразования Лапласа следующим образом:
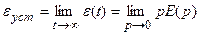 , (13.1)
, (13.1)
где E(p) - изображение сигнала ошибки e(t).
Данное равенство справедливо только для устойчивых систем автоматического управления. Так как
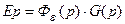 ,
,
| где | Fe(p) | – передаточная функция замкнутой системы относительно ошибки; |
| G(p) | – изображение выходного сигнала, |
то выражение (13.1) можно переписать так:
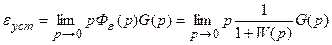 , (13.2)
, (13.2)
где W(p) - передаточная функция разомкнутой системы.
Совершенно аналогично может быть получено выражение для определения установившегося значения выходной величины:
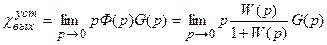 , (13.3)
, (13.3)
где Ф(р) - передаточная функция замкнутой системы по управляющему воздействию.
Рассмотрим случаи определения установившейся ошибки для статической и астатической системы при различных видах входных воздействий. Известно, что любую систему автоматического управления можно привести к одноконтурной структуре. Тогда передаточную функцию разомкнутой системы можно представить в следующем виде:
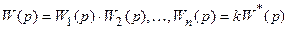 ,
,
| где | k | – передаточный коэффициент разомкнутой системы; |
| W*(p) | – передаточная функция всех остальных звеньев разомкнутой цепи с передаточным коэффициентом, равным единице. |
Статическая система в одноконтурном виде не должна содержать интегрирующих звеньев, следовательно, 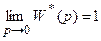 . Поэтому установившуюся ошибку статической системы (13.2) можно представить так:
. Поэтому установившуюся ошибку статической системы (13.2) можно представить так:
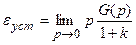 ,
,
а установившееся значение выходной координаты будет равно (13.3):
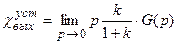 .
.
При постоянном входном воздействии, в частности, равном единичной ступенчатой функции 1(t), получаем: 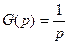 и
и
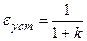 ;
; 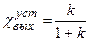 .
.
В случае постоянного воздействия, приложенного к статической системе, установившаяся ошибка называется статической ошибкой и обозначается через D. А установившаяся величина выходной координаты называется статическим отклонением.
Следовательно, для повышения точности статической системы в установившемся режиме необходимо увеличивать передаточный коэффициент системы, при этом выходная координата будет стремиться к величине входного сигнала. Однако увеличение передаточного коэффициента системы повышает ее колебательность и может привести к неустойчивости. Поэтому коэффициенты передаточной функции должны выбираться таким образом, чтобы при достаточной точности обеспечивалась необходимая устойчивость управления.
На рис.13.1,а показана установившаяся ошибка статической системы при единичном входном сигнале. Определим установившуюся ошибку статической системы при переменном входном сигнале, изменяющемся с постоянной скоростью 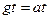 . Тогда
. Тогда 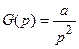 и в соответствии с (13.2), (13.3) получаем:
и в соответствии с (13.2), (13.3) получаем:
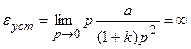 ;
;
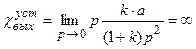 .
.
Как видно из полученных выражений, установившийся режим в системе не наступает, причем ошибка в пределе возрастает до бесконечности (рис.13.1,б).
 |
Рис.13.1. К определению установившейся ошибки статической САУ:
а - при единичном ступенчатом воздействии;
б - при линейно возрастающем воздействии
Совершенно очевидно, что статические системы не могут использоваться для регулирования таких процессов, в которых внешние воздействия носят переменный характер. В частности, статические системы не могут использоваться в качестве следящих систем.
Рассмотрим точность работы в установившемся режиме астатических систем 1-го и 2-го порядков. В астатической системе 1-го порядка передаточная функция разомкнутой системы, приведенная к одноконтурной структуре, может быть представлена в виде:
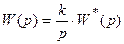 ,
,
| где | k | – постоянная, определяющая передаточный коэффициент разомкнутой системы; |
| W*(p) | – передаточная функция всех оставшихся звеньев разомкнутой системы. |
Очевидно, что 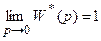 .
.
На основании (13.2), (13.3) можно записать:
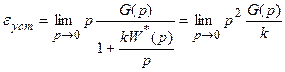 ;
;
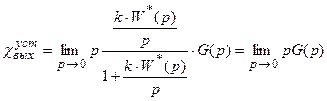 .
.
Пусть входной сигнал представляет собой единичную ступенчатую функцию 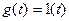 , тогда
, тогда 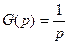 .
.
Находим:
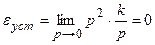 ;
;
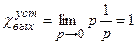 .
.
 |
Рис.13.2. К определению установившейся ошибки астатической
первого порядка САУ: а - при g(t)=at; б - при g(t)=at2
Таким образом, при действии на систему с астатизмом первого порядка (n=1) постоянного входного сигнала 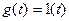 установившаяся ошибка на выходе сумматора, к которому приложен сигнал, стремится к нулю, а установившееся значение выходной координаты совпадает с входным сигналом.
установившаяся ошибка на выходе сумматора, к которому приложен сигнал, стремится к нулю, а установившееся значение выходной координаты совпадает с входным сигналом.
Пусть теперь входной сигнал имеет вид 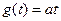 и
и 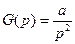 . Установившееся значение ошибки системы будет равно
. Установившееся значение ошибки системы будет равно
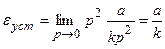 ,
,
а установившаяся величина выходной координаты определяется таким образом:
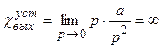 ,
,
т.е. выходная величина, как и входной сигнал, в пределе стремится к бесконечности, причем значение установившейся ошибки сохраняется постоянным: 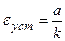 (рис.13.2,а). Уменьшить установившуюся ошибку системы можно путем увеличения передаточного коэффициента разомкнутой системы. Как было уже отмечено выше, увеличение передаточного коэффициента может привести к неустойчивости системы.
(рис.13.2,а). Уменьшить установившуюся ошибку системы можно путем увеличения передаточного коэффициента разомкнутой системы. Как было уже отмечено выше, увеличение передаточного коэффициента может привести к неустойчивости системы.
Рассмотрим теперь, как изменится установившаяся ошибка астатической системы с астатизмом первого порядка при входном воздействии вида g(t)=at2 (входной сигнал изменяется с постоянным ускорением). Изображением входного сигнала будет 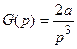 , поэтому
, поэтому
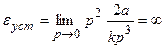 .
.
Таким образом, при заданном сигнале астатическая система с астатизмом первого порядка является практически неработоспособной (рис.13.2,б). Для осуществления процесса регулирования (слежения) при быстроменяющихся сигналах используется астатическая система с астатизмом второго порядка (n=2).
Передаточную функцию разомкнутой астатической системы с астатизмом второго порядка, приведенной к одноконтурному виду, можно представить таким образом:
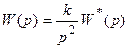 ,
,
где
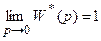 .
.
Тогда на основании (13.2) получаем
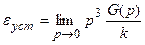 .
.
Если g(t)=at2 , то 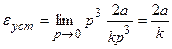 .
.
Таким образом, система отрабатывает входной сигнал вида g(t)=at2 с постоянной установившейся ошибкой. Легко определить, что установившаяся ошибка астатической системы второго порядка при входных сигналах вида 1(t), at стремится к нулю.
2. Статические и астатические системы управления
Рассмотрим систему
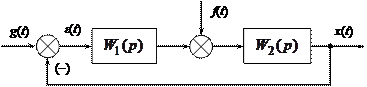 |
Рис. 13.3
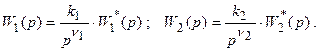
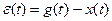 ,
,
при 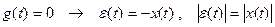
при 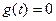 для
для 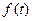 имеем
имеем 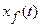
Находим
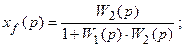
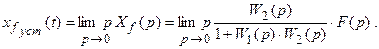
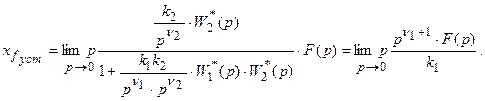
Система называется астатической по возмущающему воздействию, если передаточная функция разомкнутой системы от точки приложения задающего воздействия до точки приложения возмущения 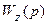 содержит полюса, равные нулю, кратность таких полюсов
содержит полюса, равные нулю, кратность таких полюсов 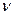 определяет порядок астатизма системы.
определяет порядок астатизма системы.
3. Чувствительность систем управления
Параметры системы автоматического управления в процессе работы не остаются равными расчетным значениям. Это объясняется изменением внешних условий, неточностью изготовления отдельных устройств системы, старением элементов и т. п. Изменение параметров САУ, т. е. изменение коэффициентов уравнений системы, вызывает изменение статических и динамических свойств системы.
Зависимость характеристик системы от изменения каких-либо ее параметров оценивают чувствительностью. Под чувствительностью понимают свойство системы изменять режим работы вследствие отклонения каких-либо параметров от номинальных значений. Для числовой оценки чувствительности используют функции чувствительности, определяемые как частные производные от координат системы или показателей качества процессов управления по вариациям параметров:
uij=(дxi/дαj)0, (13.4)
где хi — координаты системы; αj - параметр системы.
Индекс 0 означает, что функция uij вычисляется при номинальных значениях параметров.
Система, значения параметров которой равны номинальным и не имеют вариаций, называется исходной системой, а движение в ней - основным движением. Система, в которой имеют место вариации параметров, называются варьированной системой, а движение в ней - варьированным движением. Разность между варьированным и основным движениями называют дополнительным движением.
Допустим, что исходная система описывается системой нелинейных дифференциальных уравнений
dxi/dt=fi(x1,…, xn; α1,… αm), (13.5)
Пусть в некоторый момент времени в системе произошли вариации параметров Δαj, где j = 1, 2, ..., m; тогда параметры станут равными αj+Δαj. Если вариации параметров не вызывают изменения порядка уравнения, то варьированное движение описывается новой системой п уравнений первого порядка
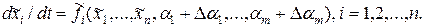 (13.6)
(13.6)
Разность решений уравнений (4.94) и (4.95) определяет дополнительное движение:
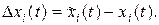 (13.6)
(13.6)
Если 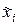 и
и 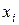 дифференцируемы по αj(j=1,…,m), то дополнительное движение (13.6) можно разложить в ряд Тейлора по степеням Δαj. При малых вариациях параметров ограничимся в разложении лишь линейными членами. Нужно отметить, что в случае конечных вариаций такое приближение недопустимо. Итак, можно записать уравнения первого приближения для дополнительного движения:
дифференцируемы по αj(j=1,…,m), то дополнительное движение (13.6) можно разложить в ряд Тейлора по степеням Δαj. При малых вариациях параметров ограничимся в разложении лишь линейными членами. Нужно отметить, что в случае конечных вариаций такое приближение недопустимо. Итак, можно записать уравнения первого приближения для дополнительного движения:
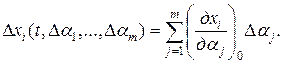 (13.7)
(13.7)
Учитывая формулу (13.4), можно записать
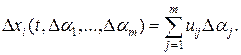 (13.8)
(13.8)
Следовательно, располагая функциями чувствительности и задаваясь вариациями параметров, можно определить первое приближение для дополнительного движения.
Продифференцируем уравнения исходной системы (13.5) по αj:
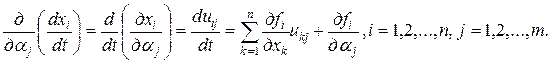 (13.9)
(13.9)
Полученные линейные дифференциальные уравнения (13.9) называются уравнениями чувствительности. Решение их дает функции чувствительности uij. Следует заметить, что в силу сложности уравнений (13.9) их решение весьма затруднительно. М. Л. Быховским предложен структурный метод построения модели для определения функций чувствительности. 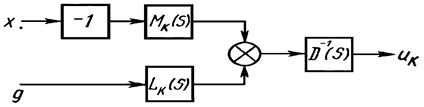
Рис. 13.4
Для определения функций чувствительности можно использовать уравнения системы или ее передаточные функции.
Пусть САУ описывается уравнением
D(p)x(t)=K(p)g(t), (13.10)
где D(p)=pn+α1 (α1,…,αk)pn-1+…+an(α1,…,αk) - собственный оператор системы;
K(p)=pm+b1 (α1,…,αk)pm-1+…+bn(α1,…,αk) - оператор воздействия g(t); p=d/dt; n≥m.
Запишем уравнения чувствительности, продифференцировав (13.10) по αk:
D(p)uk=Lk(p)g – Mk(p)x (13.11)
при t = 0;
piuk=0; Lk(p)=dK(p)/dαk; Mk(p)=dD(p)/dαk.
По уравнению (13.11) можно представить структурную схему модели чувствительности для определения функции uk (рис. 13.4). Эту схему можно упростить.
| <== предыдущая лекция | | | следующая лекция ==> |
| Методика построения логарифмических частотных характеристик разомкнутой САУ. | | | по вещественной частотной характеристике |
Дата добавления: 2016-06-24; просмотров: 11717;
