по вещественной частотной характеристике

Приближенная оценка качества САУ

Частотные методы анализа качества процесса управления основаны на известной зависимости между переходной и вещественной частотной характеристиками замкнутой системы

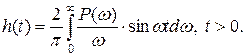(14.1)

Эта зависимость позволяет точно определить переходную функцию исследуемой системы, однако вычисление интеграла (14.1) связано с определенными трудностями. Поэтому большую роль приобретают приближенные способы оценки качества процесса управления и построения кривой переходного процесса по вещественной частотной характеристике замкнутой системы без вычисления этого интеграла.

Важный вклад в решение этой задачи был сделан известным советским ученым В.В. Солодовниковым. В дальнейшем будут рассмотрены следующие вопросы:

- приближенная оценка качества процесса управления по вещественной частотной характеристике замкнутой системы;

- приближенный метод построения кривой переходного процесса при помощи типовых трапецеидальных частотных характеристик;

- определение вещественной частотной характеристики замкнутой системы по логарифмическим частотным характеристикам разомкнутой системы.

На основании исследования связи (14.1) получены зависимости между свойствами вещественной частотной характеристики замкнутой системы и ее переходной функцией, позволяющие оценивать качество переходного процесса. Рассмотрим основные зависимости.

I. Свойство линейности.

Это свойство основывается на возможности представления подынтегрального выражения (14.1) в виде суммы составляющих за счет замены

Тогда и переходная функция системы может рассматриваться как сумма отдельных составляющих:

где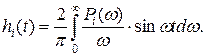

Это свойство может позволить существенно упростить процесс определения переходной характеристики системы, если для каждой составляющей вещественной частотной характеристики Р_i(w) (i= 1, 2, ..., n) переходная функция h_i(t) известна или может быть легко вычислена.

2. Изменение масштаба вдоль оси ординат.

Так как от умножения обеих частей зависимости (14.1) на число п равенство не нарушается, это означает, что при изменении масштаба вещественной частотной характеристики вдоль оси ординат величина соответствующей ей переходной функции вдоль оси ординат изменяется во столько же раз (рис. 14.1).

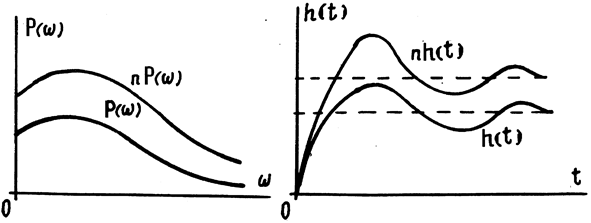
Рис.14.1. К определению влияния изменения масштаба

вдоль оси ординат P(w) на h(t)

3. Изменение масштаба вдоль оси абсцисс.

Пусть имеем

(а)

На основании (14.1) можно записать:

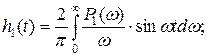
Для того чтобы выяснить соотношения аргументов переходных функций из условия выполнения равенства h₁(t₁)=h₂(t₂), проведем замену переменной интегрирования w=w₁n и приравняем правые части вышеуказанных выражений:

Далее получаем

Из условия выполнения этого равенства находим

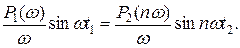
Учитывая зависимость (а), получаем 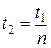. Таким образом, справедливо соотношение .

Следовательно, при увеличении (уменьшении) масштаба вещественной частотной характеристики вдоль оси абсцисс масштаб переходной функции уменьшается (увеличивается) в такое же число раз (рис. 14.2). Это означает, что при расширении полосы частот вещественной частотной характеристики системы переходный процесс в ней протекает быстрее.

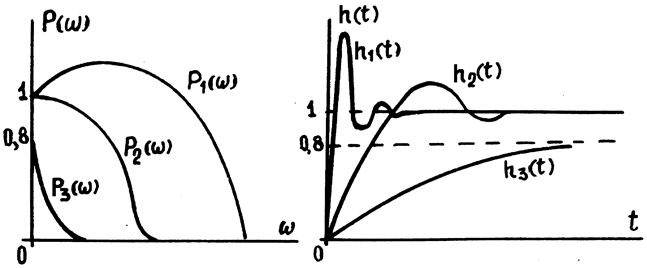
Рис.14.2. К определению влияния изменения масштаба

вдоль оси частот P(w) на h(t)

4. Определение конечного значения переходной функции по вещественной частотной характеристике.

По теореме о конечном значении функцииимеем

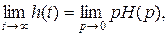(б)

где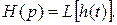

С другой стороны,

где 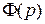- передаточная функция замкнутой системы, а

Учитывая (б) и заменяя p=jw , получаем

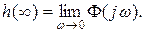
Но так как

то находим

Таким образом, конечное значение переходной функции равно начальному значению вещественной частотной характеристики. Например, для статической системы передаточную функцию разомкнутой системы можно представить следующим образом:

причем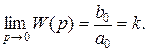

Тогда можно найти

Если система астатическая с передаточной функцией разомкнутой системы

На рис.14.3,а показан характер изменения вещественной частотной характеристики замкнутой системы по управляющему воздействию для случаев статического и астатического регулирования. Аналогично могут быть определены значения Р(0) передаточной функции замкнутой системы относительно возмущающего воздействия и для сигнала ошибки (рис.14.3,б, в).

5. Определение начального значения переходной функции по вещественной частотной характеристике.

Аналогично предыдущему, используя теорему операционного исчисления с начальным значением функции, можно получить

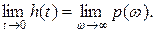
Необходимо отметить, что если порядок числителя Ф(jw) меньше порядка знаменателя, то

Рис.14.3. К определению конечного значения h(t) по P(w) САУ

и разрыв непрерывности P(w):

а) по управляющему воздействию; б) по возмущающему воздействию;

в) по сигналу ошибки; г) разрыв непрерывности P(w)

В противном случае, когда порядки числителя и знаменателя одинаковы,

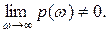
Например, имеем

На рис.14.4 показано соответствие между начальным и конечным значениями вещественной частотной характеристики p(w) и переходной функции h(t).

6. Разрывы непрерывности и пики в вещественной частотной характеристике.

На рис. 14.3,г показана вещественная частотная характеристика замкнутой системы P₁(w) которая при w=w_i претерпевает разрыв и устремляется к бесконечности. Это означает, что комплексный коэффициент передачи замкнутой системы имеет полюс, равный величине j(w) , т.е.

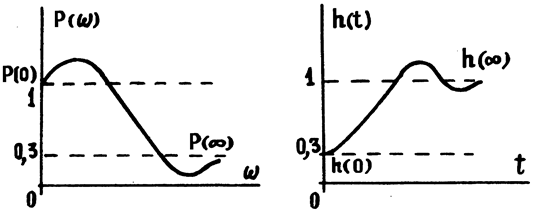
Рис.14.4. К определению начального значения h(t) по P(w) САУ

Так как вещественная частотная характеристика устремляется в бесконечность при w=0, то это говорит о наличии нулевого корня в характеристическом уравнении системы. Поэтому система в этом случае будет нейтрально устойчивой. Очевидно, если криваяp(w) имеет явно выраженныепики, то это характеризует склонность системы к колебаниям, что является весьма нежелательным.

7. Оценка перерегулирования по виду вещественной частотной характеристики.

Если экстремумы вещественной частотной характеристики могут определять склонность системы к колебательности, то их отсутствие должно характеризовать ограниченность возможных колебаний в системе. Было доказано, что если вещественная частотная характеристика Р(w) представляет собой положительную функцию от w для всех значений частоты, т.е. выполняется условие

то перерегулирование при единичном ступенчатом воздействиине превысит 18% (рис. 14.5,а).

8. Условия монотонного протекания переходного процесса (достаточные условия).

Эти условия заключаются в следующем: переходный процесс будет монотонным, если вещественная частотная характеристика представляет собой непрерывную положительную функцию от w с отрицательной производной , монотонно убывающей по абсолютной величине (рис. 14.5,б).

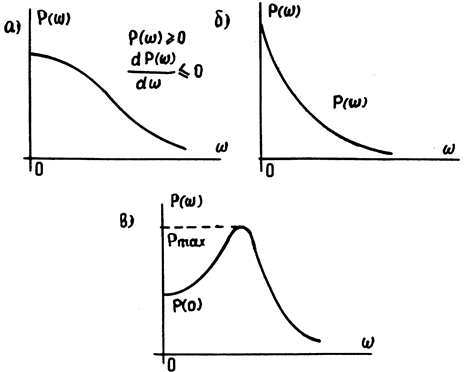
Рис. 14.5. Оценка регулирования по виду Р(w) САУ:

а, в) оценки перерегулирования; б) монотонность

9. Определение верхнего предела для величины перерегулирования при наличии максимума в вещественной частотной характеристике.

Верхний предел перерегулирования s % определяется таким образом:

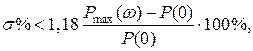
где - соответственно максимальное и нулевое начальные значения ординат вещественной частотной характеристики (рис. 14.5,в).

10. Оценка нижнего предела для времени переходного процесса T_p по величине интервала положительности w_П

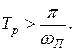
Интервал положительности w_П находится из условия Р(w)>0 .

11. Достаточно близким переходным процессам соответствуют близкие частотные характеристики.

Поэтому при определении переходного процесса по заданной вещественной частотной характеристике могут быть использованы типовые вещественные частотные характеристики, для которых переходные процессы заранее вычислены.

Рассмотренные выше зависимости между вещественной частотной характеристикой и переходной функцией системы, позволяющие приближенно оценить качество процесса регулирования, нашли широкое применение при исследовании систем автоматического регулирования.

14.2. Интегральные оценки качества процесса управления

Построение переходного процесса путем решения дифференциальных уравнений связано с большими вычислительными трудностями. Кроме этого в процессе таких расчетов весьма усложняется анализ влияния отдельных параметров системы на переходный процесс. Поэтому большой интерес представляют косвенные методы исследования качества систем автоматического регулирования, непосредственно не связанные с решением соответствующих дифференциальных уравнений. Среди этих методов широкое признание получили интегральные оценки переходных процессов.

Интегральные оценки качества процесса регулирования не могут дать количественных значений таких показателей переходной характеристики системы, как величина перерегулированияили максимальное отклонение регулируемой координаты, время регулирования и пр. Интегральные оценки позволяют лишь качественно характеризовать быстроту затухания переходного процесса. Это означает, что вывод о качестве переходного процесса регулирования можно сделать только путем сравнения соответствующих интегральных оценок, найденных для различных значений параметров исследуемой системы.

Различают линейные и квадратичные интегральные оценки. Линейная интегральная оценка определяется следующим образом:

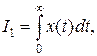(14.2)

где в качестве функции времени х(t), характеризующей течение переходных процессов в системе, могут быть использованы импульсная переходная функция w(t), переходная составляющая ошибки h_ε(∞)=h_ε(t), их производные и т.д.

Интеграл (14.2) вычисляется очень просто. Покажем это. Если функция х(t) является абсолютно интегрируемой, т.е. 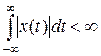, то можно получить ее изображение по Лапласу

Сравнивая с (14.2), находим

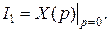
Таким образом, для определения I₁ достаточно вычислить изображение по Лапласу соответствующей функции времени при р=0, не решая дифференциального уравнения. Линейная интегральная оценка может использоваться лить для исследования систем, имеющих монотонный переходный процесс (рис.14.6,а). Действительно, в этом случае при уменьшении I₁ уменьшается время переходного процесса, т.е. быстродействие системы возрастает. Поэтому при синтезе систем, если заранее известно, что переходные процессы в них могут иметь только монотонный характер, выбор параметров регулятора следует проводить из условия минимума I₁ .

Если же кривая переходного процесса имеет колебательный характер (рис.14.6,б), то линейная интегральная оценка может оказаться неприемлемой. На самом деле, при слабо затухающем переходном процессе интеграл может быть близок к нулю, в то время как система в виду высокой колебательности является неработоспособной. При исследовании систем форма переходного процесса заранее неизвестна, поэтому применение линейной интегральной оценки качества процесса регулирования оказывается практически нецелесообразным.

Рис.14.6. Линейная интегральная оценка

Квадратичные интегральные оценки не имеют указанного выше недостатка и поэтому могут использоваться для оценки качества системы при колебательном переходном процессе. В качестве квадратичной интегральной оценки А.А. Харкевичем был предложен следующий интеграл:

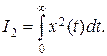(14.3)

Геометрически он представляет собой площадь под кривой квадратов ординат переходного процесса (рис. 14.7).

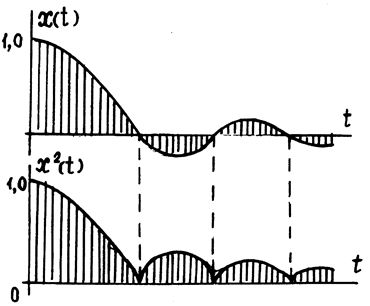
Рис.14.7. Квадратичная интегральная оценка

14.3. Корневые методы оценки качества регулирования

Известно, что характер переходного процесса в системе определяют по ее реакции на единичное ступенчатое воздействие. Переходная характеристика h(t) системы может быть вычислена с помощью обратного преобразования Лапласа (по формулам разложения Хевисайда):

Если D(s) не имеет кратных корней, то

(14.4)

где s_i — корни характеристического полинома замкнутой системы D(s)=0; — первая производная характеристического полинома D(s) по s при s=s_i.

Из (14.4) видно, что на характер переходного процесса влияют и числитель и знаменатель передаточной функции замкнутой системы W_gs(s). Если числитель W_gs(s) не имеет нулей, т. е. представляет собой постоянную величину, то характер переходных процессов можно оценить по ее полюсам, т.е. корням характеристического уравнения замкнутой САУ D(s)=0.

Для приближенной оценки качества переходного процесса в системе нужно на плоскости корней s выделить область, в которой располагаются корни ее характеристического уравнения. Чаще всего эту область представляют трапецией (рис. 14.8). Корни характеристического уравнения располагаются внутри этой трапеции АВСD, на ее сторонах и основаниях хотя бы по одному корню, а вне ее - ни одного. Для выделения этой области на плоскости корней вычисляют параметры: степень устойчивости η, колебательность μ и значение ξ вещественной части максимально удаленного корня от мнимой оси.

Понятие степени устойчивости η введено Я. 3. Цыпкиным и П. В. Бромбергом. Степенью устойчивости η называют расстояние от мнимой оси до ближайшего корня или ближайшей пары сопряженных комплексных корней. Степень устойчивости η определяет ближайшее к мнимой оси основание трапеции АD (рис. 14.8).

Пусть общее решение дифференциального уравнения системы

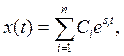(14.5)

где s_i — корни характеристического уравнения D(s)=0.

Составляющая этого решения, определяемая степенью устойчивости, запишется в виде

(14.6)

для случая вещественных корней или

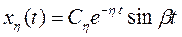(14.7)

для случая, когда среди корней есть пара комплексно-сопряженных.

В большинстве случаев переходный процесс можно считать закончившимся тогда, когда затухнет составляющая переходного процесса, определяемая степенью устойчивости, т.е. порядок величины времени затухания процесса можно грубо оценить по наиболее медленно затухающей составляющей xη(t) [см. (14.6), (14.7)]. В случае, когда ближайшим к мнимой оси является вещественный корень, из (14.6) можно получить следующую зависимость: . Если принять, например, Δ=0,05, то время переходного 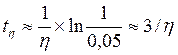. В том случае, когда ближайшей к мнимой оси является пара комплексных корней, из (14.7) можно найти верхнюю границу времени переходного процесса: .

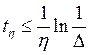Можно поставить две задачи:

1. По заданным параметрам системы - коэффициентам D(s) - определить степень устойчивости системы (задача анализа степени устойчивости).

2. По заданной степени устойчивости определить значение варьируемых параметров системы (задача синтеза САУ по заданной степени устойчивости).

Воспользуемся методом, изложенным в [1]. Предлагается сместить мнимую ось влево на величину η, тогда один корень окажется на мнимой оси, а система - на границе устойчивости. Это соответствует обращению в нуль старшего определителя Гурвица: Δ_n=a_n·Δ_n_-1=0. Это условие дает уравнение, по которому, задаваясь коэффициентами, можно определить η или решить обратную задачу.

Пусть характеристическое уравнение системы

D(s)=a₀sⁿ+ a₁sⁿ^-1+…+ a_n_-1s+ a_n=0.

Введем новую переменную z=s+η. Подставив значение s=z-η в уравнение D(s)=0, получим новое смещенное уравнение:

A₀zⁿ+A₁z^n-1+…+ A_n-1z+ A_n=0, (14.8)

где

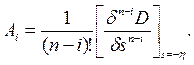(14.9)

Если в смещенном уравнении окажется A_n=0, то ближайшим к мнимой оси окажется нулевой корень, а если A_n≠0, то - пара сопряженных комплексных корней.

Условие границы устойчивости для системы, описанной уравнением (14.8), по критерию Гурвица Δ_n_-1=0 при соблюдении всех остальных условий устойчивости Гурвица.

Колебательностью системы μ называют тангенс угла, образованного отрицательной вещественной полуосью и лучом из начала координат к корню, у которого отношение мнимой части к действительной максимально (рис. 14.8):

μ=tgφ=(β/α)_max, (4.10)

где β — значение мнимой части корней D(s); α — действительная часть.

При известных параметрах системы можно определять значение колебательности μ (задача анализа колебательности) или решать обратную задачу - задачу синтеза САУ по заданной колебательности. Для этого в характеристическое уравнение системы вводится замена 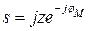, равноценная повороту мнимой оси на угол (π/2 — φ_M), при этом пара сопряженных комплексных корней окажется на мнимой оси, а фиктивная система - на границе устойчивости. Колебательность μ является оценкой переходного процесса сверху, при увеличении μ возрастает число колебаний п за время регулирования и возрастает перерегулирование.

<== предыдущая лекция	\|	следующая лекция ==>
Оценка точности САУ в установившемся режиме	\|	Общие принципы коррекции динамических свойств СУ

Дата добавления: 2016-06-24; просмотров: 3676;