Доказательство теоремы

Используем разложение многочлена Q(P) на простые двучлены и трехчлены. Каждому вещественному корню 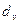соответствует двучлен 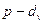, каждой паре комплексно сопряженных корней 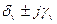- трехчлен 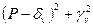, если все 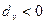, , 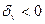то коэффициенты во всех двучленах и трехчленах положительны, а следовательно, положительны и коэффициенты в многочлене Q(P), Являющимся их произведением.

Пример 1 Многочлен 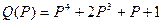, заведомо неустойчив, поскольку коэффициент при P₂ равен нулю.

Выполнение условия необходимости, не гарантирует устойчивости многочлена при любом n, хотя оно достаточно при n=1, и n=2. При больших (n>2) приходится использовать более сложные процедуры. Кроме того, как известно из алгебры для уравнений 3 и 4 степени имеются общие формулы для нахождения корней, а для уравнений 5степени и выше таких формул нет. Поэтому для систем выше 2 порядка особенно важны условия, которые позволяли бы судить об их устойчивости, не вычисляя корней характеристического уравнения. Такие условия называются критериями устойчивости.

7.7 Критерий устойчивости Гурвица. (Гаусса – Гурвица)

Для формулировки критерия Гурвица составим из характеристического уравнения определитель n порядка.

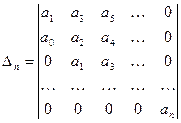
на главной диагонали, которого располагаются коэффициенты в порядке возрастания их индексов, начиная с a₁ кончая a_n. В каждом столбце при движении от элемента, находящегося на главной диагонали, вверх индексы коэффициентов возрастают, вниз убывают, при этом на месте элементов с индексами, превышающими n (при движении вверх) и отрицательными индексами (при движении вниз). Проставляются нули. Запишем частные миноры определителя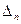

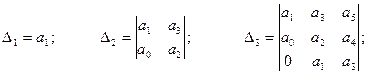и.т.д.

!!!!!!

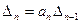Назовем эти миноры, включая определитель 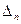, определителем Гурвица.