Критерий устойчивости Рауса.
Применение критерия требует составления таблицы Рауса. Элементы её первой строки являются четные коэффициенты характеристического уравнения, начиная с a0,a2 a4, …
Элементы последующих строк вычисляют по приведенным в таблице формулам. Причем при вычислении элементов какой-либо i-ой строки необходимо предварительно вычислить коэффициент ri. Всего в таблице заполняют n+1 строк.
Критерий формируют следующим образом: система устойчива, если все элементы первого столбца таблицы Рауса имеют одинаковый знак. Обычно характеристическое уравнение приводится к виду a0>0, тогда все элементы первого столбца должны быть положительными. Ci,1>0, i=2 ,n+1.
При наличии отрицательных элементов в первом столбце таблицы Рауса местами неустойчивы. Если один из элементов первого столбца равен 0, то системы на границе устойчивости, характеристическое уравнение имеет пару чисто мнимых корней.
При равенстве нулю последнего n+1 элемента или _____последних элементов первого столбца системы также на границе устойчивости.
Составляя таблицу Рауса, расчет можно сразу заменить при появлении первого нулевого или отрицательного элемента на первом столбце, т.к. система на границе устойчивости или неустойчива.
| Вспомогательные коэффициенты | № строки | `№ столбца. | |||
| - | C11=a0 | C21=a2 | C13=a4 | ||
| - | C21=a1 | C22=a3 | C23=a5 | ||
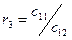
| C31= C12+ r3C22 | C32= C13+ r3C23 | C33= C14+ r3C24 | ||
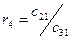
| C41= C22+ r4C32 | C42= C23+ r4C33 | C43= C24+ r4C34 | ||
| ----- | ----- | ----- | ----- | ----- | |
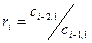
| i | Ci1= Ci-2,2+ riCi-1,2 | Ci2= Ci-2,3+ riCi-1,3 | Ci3= Ci-2,4+ riCi-1,3 | |
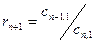
| n+1 | Ci,n+1= Cn-1,-2+ rn+1Cn,2 | - | - |
Дата добавления: 2016-11-28; просмотров: 1066;