Влияние звена чистого запаздывания на устойчивость.

Чистое запаздывание – это часть системы (цепь или блок), при прохождении которой сигнал не меняет своей формы, но задерживается на время T.

Типичный пример: локальная сеть без потерь или длинная линия, или транспортная задержка.

Покажем, что такому преобразованию соответствует передаточная функция; для этого вычислим преобразование Лапласа выходного сигнала:

Wзап(p)=e-pτ;

Таким образом, звену чистого запаздывания соответствует передаточная функция, не являющаяся дробно-рациональной. Она трансцендентная.

Рассмотрим АФЧХ - частотную характеристику звена чистого запаздывания:

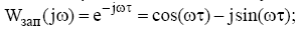
При любом w получается точка единичной окружности.

АЧХ: |Wзап(jω)| = 1;

ФЧХ:ϕ(ω)= -ωτ;

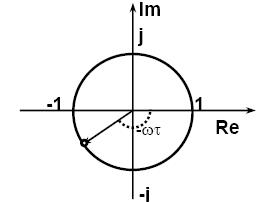
Рисунок 8‑7

Видим, что звено чистого запаздывания добавляет отрицательный фазовый сдвиг, -1 1тем больший, чем больше частота, темсамым уменьшая запас устойчивости по фазе. За счет этого сдвига система вполне может стать неустойчивой.

К сожалению, подобным образом нельзя описать запаздывание, зависящее от времени.

Фактически, мы ввели еще один стандартный блок, который можно было бы включить в стандартные звенья, если бы оно имело

обычную, а не трансцендентную передаточную функцию. Полученное звено запаздывания формально является звеном бесконечного порядка, поэтому алгебраические методы исследования устойчивости системы, содержащей звенья запаздывания неприменимы.

Пример:Охватим инерционное звено ООС с запаздыванием на время τ.

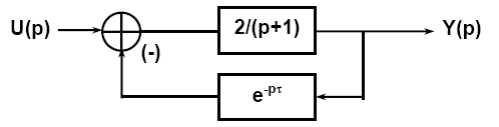
Рисунок 8‑8

Вычислим для замкнутой системы передаточную функцию и характеристический полином:

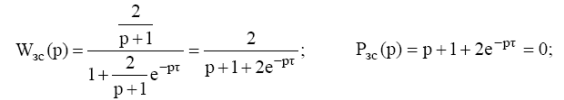У такого характеристического полинома бесконечное число корней, среди которых могут быть и корни неустойчивые, поэтому численные методы становятся бессмысленными для обоснования устойчивости. Неприменимы критерий Гурвица и необходимое условие устойчивости, а вот частотные критерии устойчивости полностью применимы.Критерий Михайлова и, вытекающий из него критерий Найквиста, позволяют вполне корректно судить об устойчивости таких систем. Найдём АФЧХ разомкнутой системы.

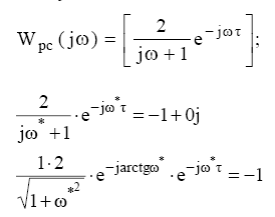
Как выяснить, при каком значении τ система (замкнутая) становится неустойчивой. Рассмотрим пограничный случай - прохождение через (-1;j0) на некоторой частоте ω*; Будем искать то минимальноезначение времени запаздывания, при котором появляется неустойчивость. Подставляем АЧХ и ФЧХ инерционного звена и звена чистого запаздывания и решаем комплексное уравнение относительно ω*и.Для этого приравняем по отдельности модуль и аргумент. Для модуля имеется следующее равенство:

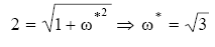
Для равенства аргументов требуется, чтобы sin(arctgω*-ω*τ)=0;Отсюда вытекает, что

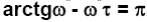
Поэтому для τ получаем:

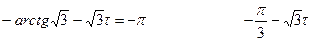
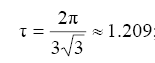
Это значение τ есть то минимальное запаздывание в нашей системе, при котором замкнутая система уже становится неустойчивой. Заметим, что звено запаздывания может располагаться и в прямой ветви, в данном случае все расчёты сохраняются.