Критерий Михайлова.
Для того чтобы система была устойчива необходимо и достаточно, чтобы кривая Михайлова, начинаясь при a0>0 с действительно положительной полуоси, при возрастании 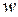 последовательно обходила n квадрантов, в положительном направлении, не попадая в начало координат (рис. 8-1).
последовательно обходила n квадрантов, в положительном направлении, не попадая в начало координат (рис. 8-1).
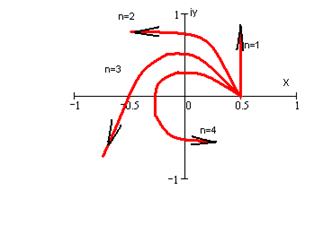
Рисунок 8‑1
Пример: Характеристический полином.
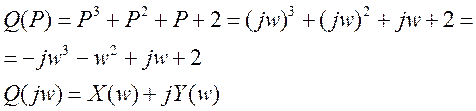
Составим таблицу
| w | 0<w<1 | 1<w< 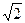
| w> 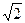
| 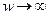
| ||
| X(w) | >0 | >0 | <0 | 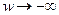
| ||
| Y(w) | >0 | <0 | <0 | 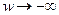
|
Построим кривую Михайлова. В пределах квадранта всей кривой Михайлова, на устойчивость не влияет, и она строится приблизительно. Система неустойчива т.к. кривая не охватывает последовательно 1, 2, и 3 квадрант.
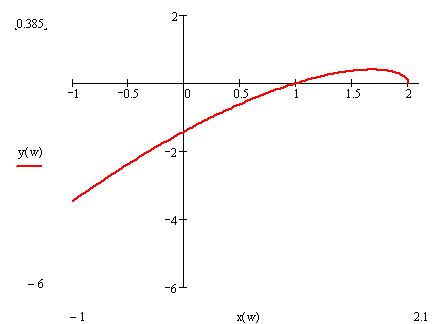
Рисунок 8‑2 – Годограф Михайлова
Пример. Характеристический многочлен 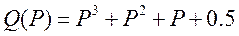
Для 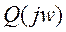 имеем
имеем 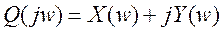
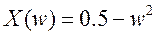 ,
, 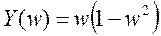
Составим таблицу
| w | 0<w< 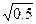
| 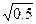
| 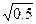 <w<1 <w<1
| 1 | w>1 | 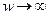
| |
| X(w) | 0,5 | >0 | <0 | -0,5 | <0 | 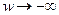
| |
| Y(w) | >0 | 0,35 | >0 | <0 | 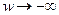
|
Построим кривую Михайлова
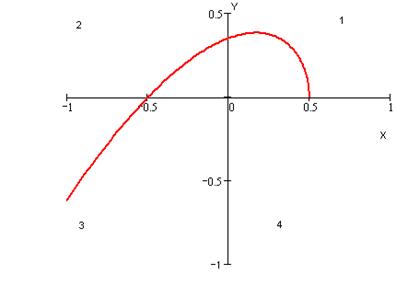
Рисунок 8‑3 Годограф Михайлова
Кривая последовательно охватывает все 3 квадранта, следовательно, система будет устойчивой.
Алгебраические критерии устойчивости и критерий Михайлова применимы для исследования замкнутой и разомкнутой систем.
Есть критерий, который предназначен для исследования лишь замкнутых систем. Этот критерий был сформулирован Найквистом.
Критерий Найквиста пусть l корней разомкнутой системы находятся в правой полуплоскости а остальные n-l в левой полуплоскости. Тогда, для того, чтобы
Замкнутая система была устойчивой необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика её разомкнутой системы с ростом w от 0 до 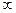 охватывала точку (-1,j0) в положительном направлении, т.е. против движения часовой стрелки в (l /2) раз.
охватывала точку (-1,j0) в положительном направлении, т.е. против движения часовой стрелки в (l /2) раз.
В частности если разомкнутая система устойчива (и, следовательно, l=0), то для того, чтобы замкнутая система была устойчива необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика её разомкнутой системы охватывала точку (-1, j0) в положительном направлении l/2 раза.
Пример: частотная передаточная функция её разомкнутой системы 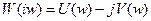
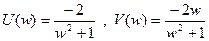
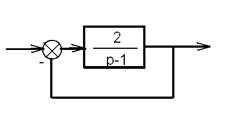
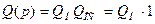
Составим таблицу.
| w | w>0 | 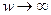
| |
| U(w) | -2 | <0 | 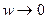
|
| V(w) | <10 | 
|
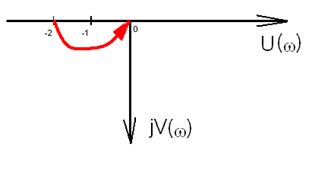
Рисунок 8‑4
Амплитудно – фазовая частотная характеристика разомкнутой системы охватывает точку (-1, j0) в положительном направлении ½ раза. Характеристическое уравнение разомкнутой системы имеет 1 корень, т.е. l=1, поэтому замкнутая система устойчива.
Примеры:
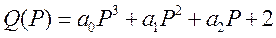
Варианты:
| a0 | a1 | a2 | a3 |
Дата добавления: 2016-11-28; просмотров: 1247;
