Понятие функции Грина
Чтобы решить уравнение 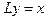 , где L= p линейный дифференциальный оператор. Предположим, что мы нашли оператор, обратный к L (обозначим его через L-1 ), такой что
, где L= p линейный дифференциальный оператор. Предположим, что мы нашли оператор, обратный к L (обозначим его через L-1 ), такой что 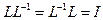 (где I - тождественный оператор). Например, если
(где I - тождественный оператор). Например, если 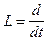 , то L-1 является оператором интегрирования
, то L-1 является оператором интегрирования  ;
; 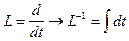 .
.
Для дифференциального оператора общего вида можно предположить, что L-1 представляет собой интегральный оператор с ядром 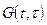 , то есть
, то есть
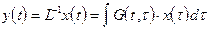 1.
1.
Если найдено ядро G, то с помощью этого равенства можно найти решение дифференциального уравнения. Причем 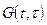 - это функция Грина, которая является очень полезным понятием. Это мы раскроем чуть позже.
- это функция Грина, которая является очень полезным понятием. Это мы раскроем чуть позже.
Действуя вновь оператором по (1), получаем
 2.
2.
Поскольку оператор интегрирования и дифференцирования являются линейными, то их можно поменять местами. Тогда первая часть
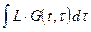 3.
3.
И поскольку слева, очевидно стоит  , то получаем
, то получаем
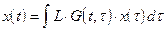 4.
4.
Известно, что 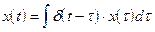 , должно иметь следующие соотношение
, должно иметь следующие соотношение

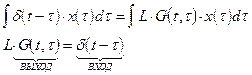 5.
5.
Из уравнения (5) вытекает очень важный факт, что ядро 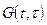 , которое называется функцией Грина, удовлетворяет тому же дифференциальному уравнению, если входное воздействие заменить на d - функцию.
, которое называется функцией Грина, удовлетворяет тому же дифференциальному уравнению, если входное воздействие заменить на d - функцию.
Оказывается функция Грина имеет простой физический смысл: это отклик на единичное импульсное воздействие
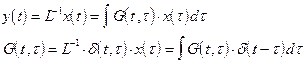
Простые системы типа "вход-выход" и функция Грина
 x(t) y(t)
x(t) y(t)


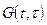


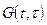


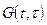
Система называется инвариантной во времени (или систем с постоянными параметрами). Если входное воздействие  возрождает отклик
возрождает отклик  .
.
Если входным сигналам x1(t) и x2(t) соответствуют выходные сигналы y1(t)и y2(t)и при этом входной сигнал 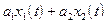 (а1 и а2 - константы) и ???? выходной сигнал
(а1 и а2 - константы) и ???? выходной сигнал 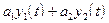 - то система называется линейной.
- то система называется линейной.

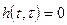 при
при 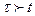 - условие физической реализуемости.
- условие физической реализуемости.
Для стационарных систем
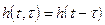 .
.
Дата добавления: 2016-11-28; просмотров: 1433;
