Передаточная функция для ошибки по помехе.

Системы автоматического управления работают, как правило, в условиях помех. При этом задающее воздействие g(t) всегда приложено к входу системы, а помеха V(t) может быть приложена в произвольной точке системы, как показано на рисунке. Разомкнутый контур разделен на две части. W₁(p)- не подвержена воздействию помех, а на входе второй W₂(p) действует помеха V(t). При этом W(p)=W₁(p) 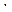W₂(p).

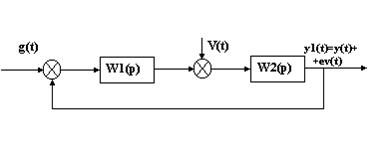
Рисунок 6‑3

Выходная величина САУ может быть представлена в виде

y₁(t)=y(t)+e_v(t) (6.19)

где y(t)=W_з(p) 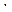g(t) - реакция системы на задающее воздействие.

E_v(t)= 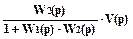(6.20)

Составляющая e_v(t) выходной величины y₁(t) искажает значение управляемой величины y(t), т.е. является ошибкой системы, обусловленной помехой V(t).

Отношение изображенияE_v(p)этой ошибки к изображению помехиV(p)определяетпередаточную функциюсистемы автоматического управлениядля ошибке по помехе:

H_ev(p) = 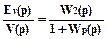(6.21)

Если помеха действует на входе системы, то получаем:

H_ev(p)= 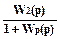=W_з (6.22)

Частотные функции

Если входное возмущение представляет собой гармоническое колебание 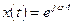, то передаточная функция превращается в частотную функцию или в частотную характеристику линейной системы

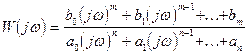; называется частотной передаточной функцией.

Ее можно представить в виде

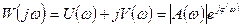6.19.

где 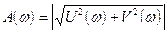; ; 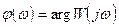6.20.

A(w)- амплитудно-частотная характеристика;

j(w)- фазочастотная характеристика.

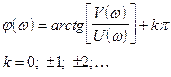
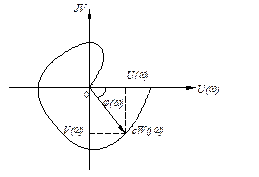
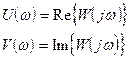
Рисунок 6‑4

На комплексной плоскости частотная передаточная функция определяет вектор 0C (длина) модуль - АЧХ, j(w)- фазочастотная характеристика. (рис 6.3)