Типовые звенья САУ.

Полиномы числителя и знаменателя передаточной функции можно разложить на простейшие множители по их корням.

здесь μ = b0/a0– константа.

Возможны два случая:

• Корни вещественные. Оставляем скобки без изменения.

• Пара комплексно сопряженных корней вида: p1,2=α ± jβ - объединяем их и раскрываем скобки (p-α+jβ)(p-α-jβ)= p2-2α p +β2 +α2 -полином имеет вещественные коэффициенты.

После такого представления в числителе и знаменателе будет некоторое количество скобок первого порядка, соответствующих вещественным корням, и некоторое количество скобок второго порядка, соответствующих комплексно – сопряженным корням. При этом все числовые коэффициенты в скобках будут вещественными.

Рассмотрим каждую такую скобку, как элементарную передаточную функцию, практически реализуемую в силу вещественности коэффициентов.

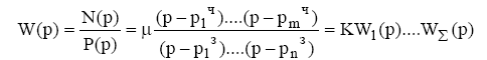(6.22)

Σ = n+m, если все корни вещественные;

Σ < n+m, если есть комплексные корни.

Принято выносить общий множитель К за скобки так , чтобы свободный член всех скобок был равен 1. Тогда К называют коэффициентом усиления. Заметим, что W(0) = К = bm/an. Это значит, что К есть коэффициент усиления на нулевой частоте -"постоянном токе".

Итак, любая Wi (р)может быть одного из следующих видов:

1. К - Усилительное звено.

2. p - Дифференцирующее звено.

3. 1/p - Интегрирующее звено (интегратор).

4. K/(Tp+1) - Инерционное (апериодическое) звено.

5. K/(T2p+2dTp+1) - Колебательное звено.

6. K(Tp+1) - Форсирующее звено.

7. K(T2p+2dTp+1) - Форсирующее звено 2-го порядка.

Замечание:

форсирующее звено (4) является комбинацией (суммой) усилителя и дифференциатора;

звенья (2), (6), (7) не является в строгом смысле реализуемыми.