Функции Грина в теории систем автоматического управления

Для описания нелинейных детерминированных систем очень полезным является понятие функции Грина.

Пусть L представляет собой операторы дифференцирования, интегрирования и умножения на константу.

Например: ;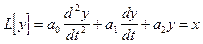

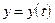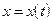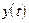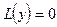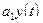где - выходной процесс, - входной процесс, a₀, a₁, a₂ - постоянные коэффициенты. Это линейные уравнения второго порядка. Видно, если - является решением уравнения , то - также решение. Если y и z - решения уравнения, то 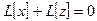и 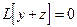, то есть

y+ z - также являются решением.

Рассмотрим x₁ решение уравнения 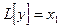и решение x₂ решение уравнения 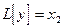. Тогда 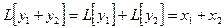. Это наш первый и очень полезный результат из которого вытекает следующее очень важное заключение:

Любое сложное входное воздействие можно представить в виде суммы составляющих, для каждой из которых уравнение можно решить отдельно. Складывая затем эти решения, можно получить решение, соответствующее полному входному воздействию .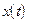

1. то есть ;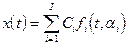

Например 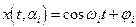- ряд Фурье.

2. можно выбрать и другой набор

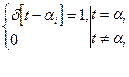
Эти импульсные функции единичной интенсивности. Отклик на такой импульс имеет характер затухающих колебаний.

Общее решение получается в результате интегрирования по всем откликам, соответствующим импульсам, которые образуют входное воздействие. В этом заключается идея метода функций Грина.