Лаплас операторы. Векторлық өрістердің классификациясы.

Екінші реттік дифференциалдық операциялар скаляр немесе векторлық өрістерге 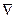операторын екі рет қолдану нәтижесінде жүзеге асырылады.

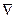Гамильтон операторының 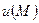скаляр өріске әсерінен 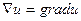векторлық өрісі пайда болады.

Егер векторлық өріске 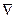операторын тағы да қолдансақ скаляр өріс аламыз:

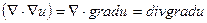(1)

және векторлық өріс алуға болады:

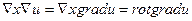(2)

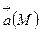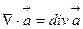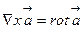Егер векторлық өрісі берілсе, онда гамильтон операторының әсерінен скаляр және векторлық өрісі туады. Гамильтон операторының векторлық өріске қайталап қолданса скалялр өріс

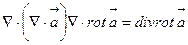(3)

және екі векторлық өрістерді:

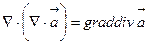(4)

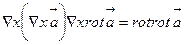(5)

(1)-(5) қатынастар екінші реттік дифференциалдық операторларды анықтайды. Осы қатынастарды қарастырайық. Скаляр өрістің градиентінің дивергенциясы:

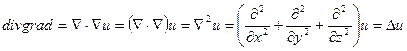(6)

мұндағы 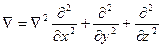-Лаплас операторы немесе лапласиан.

Сонымен қатар Лаплас операторын 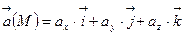векторлық өріске де қолдануға болады:

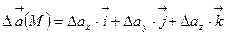(7)

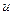скаляр өрістің градиентінің құйыны

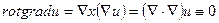(8)

себебі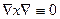

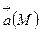векторлық өрістің құйынының дивергенциясы

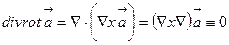(9)

себебі 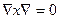Бұл кезде үш вектордың аралас көбейтіндісінің қасиеті қолданылған: 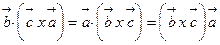біздің жағдайымызда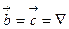

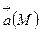векторлық өрістің құйынының құйыны:

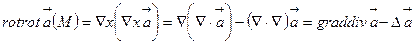(10)

мұнда мына қасиет қолданылған: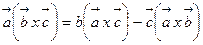

векторлық және скаляр өрістерге қолданылатын екінші реттік дифференциалдық операцияларды мынандай кесте түрінде көрсетуге болады.

	-		-
		-
		-

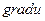
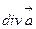
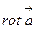
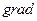
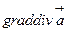
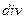
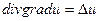
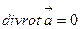
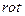
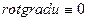
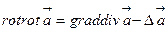
Егер кеңістіктің V облысының әрбір нүктесінде 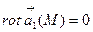болса, онда V облысында 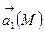векторы құйынының немесе потенциалдық деп аталады.

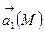өрісі тек қана 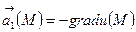болғанда құйынсыз болады мұндағы 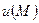-құйынсыз (потенциалдық) векторлық өрістің скалярлық потенциалы.

Шындығында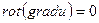

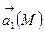векторлық өрісінің 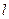контуры бойынша циркуляциясын қарастырамыз:

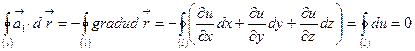
Бұл жағдайда 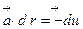толық дифференциал және мына түрдегі қисық сызықтық интеграл

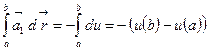интегралдың жолына тәуелсіз.

Жоғарыдағы айтылғандардың барлығы Стокс теоремасымен келіседі:

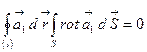
бұдан 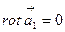екені шығады, себебі бұл теорема кез-келген контур үшін орындалады, ендеше кез-келген S бет үшін де орындалады.

Кеңістіктің берілген олблысында 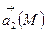векторлық өрісі соленойдтық (түтікшелік) немесе құйынды деп аталады, егер осы облыстың әрбір нүктесінде 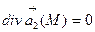болса

Векторлық өріс солленойдтық деп аталады тек 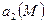- 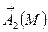векторлық өрісінің құйыны болғанда ғана, яғни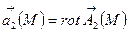

Мұндағы -соленойдтық векторлық өрістің векторлық потенциалы.

Остроградский –Гаусс теоремасын негізге ала отырып былай жазуға болады:

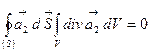
Бұдан шығатыны: кез-келген тұйық бет арқылы өтетін соленойдты векторлық өрістің ағыны нольге тең. Бұл осындай векторлық өрістің негізгі қасиеті болып табылады.

Лекция №5.