Исық сызықты ортолгональдық координаталардағы негізгі дифференциалдық операциялар.

Негізгі дифференциалдық операцияларды қисық сызықты ортолгональдық координ,аталарда өронектейміз. 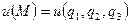скалыр өрістің градиентінің 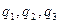қисық, сызықты координаталардағы өрнегін табамыз. 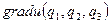векторның 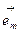бірлік векторының бағытындағы проекциясы функциясының осы бағыт бойынша туындысына тең.

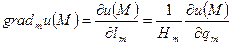
мұндағы m=1,2,3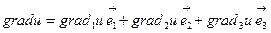

болғандықтан қисық сызықты координаталардағы скаляр өрістің градиеті:

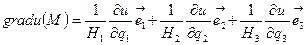(9)

Қисық сызықты координаталардағы 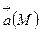векторлық өрістің дивергенциясының өрнегін анықтаймыз.

Бұл үшін 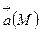векторының қисық сызықты элементар параллелепипедтің беті арқылы өтетін ағынын есептейміз және қисық сызықты координаттарда 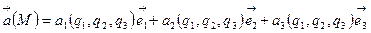екенін есептейміз.

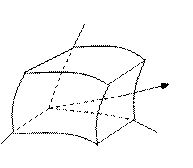
АВСД арқылы өтетін 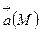векторының ағыны мынаған тең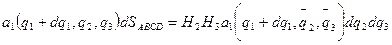

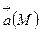векторының KMQL беті арқылы өтетін ағыны: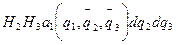

Өзара қарама-қарсы АВСД және KMQL жақтары арқылы өтетін ағындардың қосындысы:

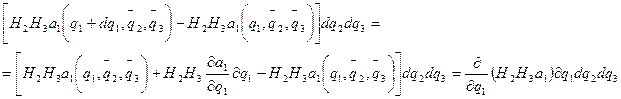
Осы әдіспен 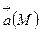векторының (АДLK, ВСQМ) және (ДС QL, АВМК) ры арқылы өтетін авғындарын анықтаймыз:

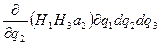және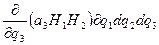

Ендеше, 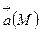векторының элементтері параллеллепипедтің барлық жақтары арқылы өтетін толық ағыны

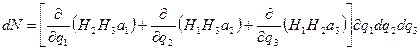
Дивергенцияның инвариантты анықтамасы бойынша: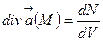

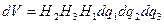
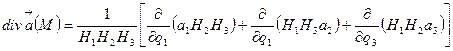(10)

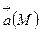векторлық өрістің құйынын есептеу үшін MQLКМ элелментар контурды қарастырамыз. Бұл контур 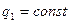жазықтығында жатыр делік.

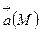векторының осы контур бойынша циркуляциясын қарастырамыз:

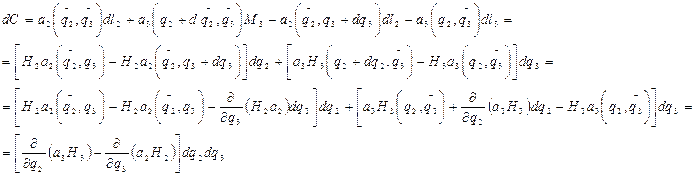
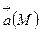векторлық өрістьің құйынының проекциясының инвариантты анықтамасын қолданамыз:

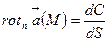
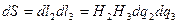екенін ескерсек

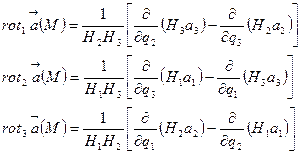
Ендеше

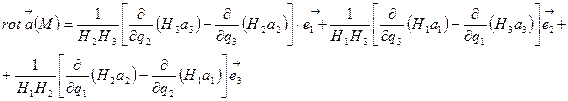
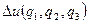операциясын қисық сызықты координаттарда алу үшін мына қатынасты қолданамыз:

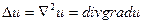
Бұл жағдайда

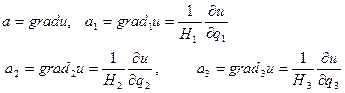
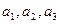-ті (10) формулаға қойып, мына өрнекті аламыз:

Лекция №7

Екінші реттік дербес туындылардағы сызықтық дифференциалдық теңдеулердің түрлері. Математикалық физиканың негізгі теңдеулері.

Теориялық физикада дербес туындылардағы дифференциалдық теңдеулер өте маңызды роль атқарады. Оның себебі, кез келген физикалық заңда тек теңдеу түрінде ғана дәл өрнектеуге болады және осы теңдеуді негізге ала отырып барлық құбылыстар мен тәжірибе қорытындыларын түсіндіруге болады. Сонымен бірге дұрыс жазылған физикалық занның дифференциалдық өрнегі әлі ашылмаған құбылыстар жайында болжам жасауға мүмкіндік береді.

Көптеген физикалық заңдардың (мысалы, кванттық механика заңдары ) өте күрделі, ерекше екенін және оларды моделдердің немесе классикалық ұқсастық өту керек. Мұндай жағдайларда оларды теңдеулер негізінде сипаттау жалғыз мүмкіндік болып табылады. Тек осындай әдіс бізге көз алдымызға елестету мүмкін емес нәрселерді түсінуге мүмкіндік береді.

Дербес туындылардағы дифференциадық теңдеу деп 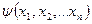белгісіз функциясын, 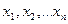тәуелсіз айнымалылары және 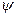функциясының дербес туындыларын байланыстыратын теңдеуді айтады.

Теңдеудің реті деп осы тендеуге енетін жоғары туындының ретін айтады.

Егер барлық туындылар мен белгісіз функцияның өзі теңдеуге бірінші дәрежемен кіретін болса, онда теңдеу сызықтық деп аталады.

Теңдеудегі орнына қойылғанда оны теңдікке айналдыратын кез келген функция теңдеудің шешімі деп аталады.

Егер 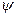функциясы теңдеудің шешімі және С 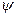да- сол теңдеудің шешімі болса, онда берілген теңдеу бір текті деп аталады (С- кез келген тұрақты), кері жағдайда- бір текті емес.

Екінші реттік сызықтық дифференциалдық теңдеулер физикада өте жие қолданылады.

n тәуелсіз айнымалылар үшін осындай теңдеудің ең жалпы түрі былай жазылады:

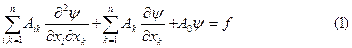
Алдағы уақытта біз 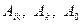коэффициенттері тұрақты сандар болатын теңдеулерді ғана қарастырамыз

Сонымен бірге 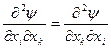болғандықтан, 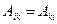деп есептеуге болады.

(1) теңдеудің шешімдерінің қасиеттері жоғары туындылардың жанында тұрған коэффициентерге байланысты болады екен. Осы коэффициенттерді мәндеріне (және олардың арасындағы қатынасқа) байланысты теңдеулер бірнеше типтерге бөлінеді. Мұны екі тәуелсіз айнымарылардын қарапайым мысалында дәлірек қарастырамыз. Берілген жағдайда (1) теңдеу былай жазылады

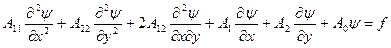(2)

Ары қарай ыңғайлы болу үшін 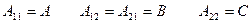деп белгілейміз. Жоғары туындылардың жанын да тұрған коэффициенттерді матрица түрінде жазамыз:

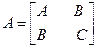
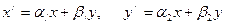түрінде тәуелсіз айнымалыларды алмастыра отырып (2) теңдеуді 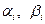тұрақтыларды сәйкестіре таңдап мына түрге келтуріге болады:

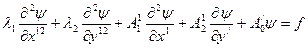
бұл теңдеуде аралас туындылар жоқ ; оны канондық деп атайды, осындағы жоғарғы туындылардың коэффициентерінің матрицасы диагональдық болады, яғни

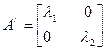
Теңдеудің түрі А матрицасының характеристикалық саны деп аталатын 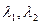сандарының мәндерімен анықталады. Оны 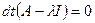теңдеуінен анықтауға болады. Біздің жағдайымызда бұл теңдеу былай жазылады:

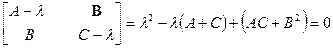
Бұдан шығатыны

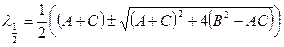
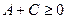болсын. Бұл теңсіздік үш жағдайда мүмкін:

1. 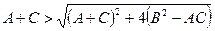, яғни 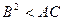болғанда. Бұл кезде екі 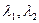түбір де оң болады, ал (2) теңдеу эллипстик типтегі теңдеу деп аталады.

2. 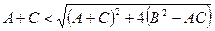, яғни 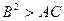, сондықтан 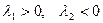, ал (2) теңдеу гиперболалық типтегі теңдеу деп аталады.

3. 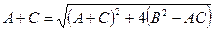, яғни 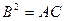, 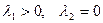(2) теңдеу параболалық типтегі теңдеу деп аталады.

Осыдан, берілген жеке жағдайда теңдеудің типі 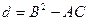дискриминантының мәнімен анықталатыны көрініп тұр.

Жалпы n тәуелсіз айнымалылар жағдайында λ; характеристикалық сандары осыған ұқсас табылады. Әрине, мұнда мүмкіндіктер көп, себебі

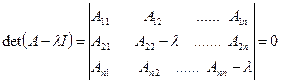
характеристикалық теңдеудің n түбірі бар, және теңдеулердің типтері көп болуы мүмкін.

Осы уақытқа дейінгі барлық белгілі физикалық есептер жоғарыда көрсетілген теңдеулердің үш типіне келтіреді:

1) эллипстік, немесе (n,0,0) типтегі, егер барлық түбірлер 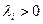болса;

2) гиперболалық, немесе (n-1, 1,0) типтегі, егер n-1 түбір оң, ол бір түбір теріс болса;

3) параболалық, немесе (n-1,0,1), егер n-1 түбір оң, ал біреуі ноль болса.

Егер (1) теңдеудің екі жағын да -1-ге көбейтсек, онда характеристикалық сондар таңбасын өзгертеді, және сол себепті, n₁ және n₂, жәнесандары орындарын ауыстырады. Бұдан (n₁, n₂, n₃) және (n₂, n₁, n₃) типтегі теңдеулердің теңбе-тен (бірдей) екендігі шығады.

Мысалы, эллипстік типтегі теңдеу үшін барлық 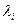; оң немесе барлығы теріс (яғни таңбалары бірдей). Осы сияқты (n-1,1,0) немесе (1,n-1,0) типтегі теңдеулер гиперболалық типтегі болып табылады ( Барлық λ; түбірлер нольге тең емес, сонымен бірге олардың (n-1)- інің таңбасы бірдей, ал біреуінікі – қарама-қарсы). Егер бір түбір нольдік, ал қалғандарының барлығының таңбасы бірдей, яғни (n-1,0,1) немесе (0,n-1,1) болса, онда параболалық типтегі теңдеу болады.

Физикалық қосымшаларда ең көп кездесетін теңдеулерді мысалға келтірейік.

1). Үш өлшемді толқындық теңдеу.

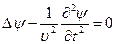(3)

мұндағы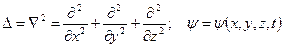

Бұл теңдеудің дербес жағдайы бір өлшемді толқындық теңдеу ( шектің тербеліс теңдеуі) болып табылады.

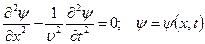(4)

2). Д, Аламбер теңдеуі (бір текті емес толқындық теңдеу)

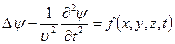(5)

3). Жылу өткізгіштіктің теңдеуі (диффузия теңдеуі)

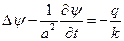(6)

Егер 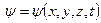- температура болса, онда 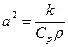, мұндағы q– температура өткізгіштік, коэффиценті ; k- жылу өткізгіштік коэффициенті, Ср- меншікті жылу сыйымдылық ; д- ортаның тығыздығы.

4). Лаплас және Пуассон теңдеулері;

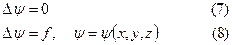
5). Шредингердің жалпы теңдеуі;

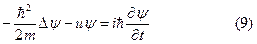
Мұндағы 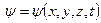; u -берілген функция, 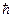-Планк тұрақтысы.

6). Шредингердің стационар теңдеуі ;

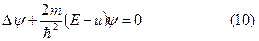
мұндағы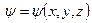

Бұл теңдеулердің барлығы сызықтық, екінші реттік. (3)-(5)- гиперболалық, (7),(8),(9)- эллипстік типтегі теңдеулер. (5),(8) теңдеулер-бір текті емес, қалғандар –бір текті.

Шредингер теңдеуін (9) ерекшелеп қарастырайық.. бұл теңдеуде уақыт бойынша бірінші туынды бар, яғни 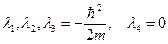, сондықтан оны парабалалық типтегі теңдеулерге жатқызуға болады. Бірақ оның шешімінің қасиеттері (3)- толқындық теңдеудің шешімдерінің қасиеттеріне ұқсас ( оның себебі, 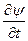-нің алдындағы коэффициент жалған).

Параболық типтегі теңдеулер барлық жағдайда «диффузиялық, яғни қайтымсыз процестерді сипаттайды.

(3) және (9) теңдеулердің уақытқа периодты тәуелді дербес шешімдерді бар, яғни 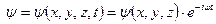. Сонымен бірге 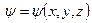функцияның кординаттық бөлігі үші екі жағдайда да бір түрдегі теңдеуді аламыз:

мұндағы 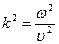(3)- теңдеу үшін және (9) теңдеу үшін. Міне сондықтан (9) теңдеуді Шредингердің толқындық теңдеуі деп атайды.

Лекция №8.

Математикалық физиканың кейбір теңдеулерін