Ақпаратты криптографиялық қорғаудың негізгі түсініктері
Ақпаратты шифрлаудың әдістері мен тәсілдерін зерттеумен айналысатын ғылым саласын криптография деп атайды [1,9-11,13-16]. Криптография ерте заманнан бері хабарламаны құпия жасау үшін қолданылып келген болатын. «Криптография» деген сөз гректің «криптос –құпия» және «графия – жазу» деген сөздерінен құралған. Деректерді қорғау үшін, бөтен адамдардың қолын жеткізбеу мақсатында деректерді өзгертуге бағытталған әдістердің жиыны криптография деп аталынады. Мұндай өзгертулер деректерді қорғаудың негізгі үш проблемасын шешуге бағытталған: құпиялықты, тұтастықты және сенімділікті.
Төменде криптографиялық жүйелердің қысқартылған схемасы көрсетілген (5.1 – ші сурет):
| алғашқы мәтін |
| шифрлау |
| шифрланған мәтін |
| байланыс арнасы |
| шифрды ашу |
| алғашқы мәтін |
k2
| кілттермен алмасу арнасы |
| кілттерді генерациялау |
12.1 сурет - Криптографиялық жүйенің қысқартылған схемасы
Криптография қолданбалы ғылым саласына жатады. Ол фундаменталды ғылым салаларының соңғы жетістіктерін пайдаланады. Олардың ішіндегі ең негізгісі математика болып табылады. Математиканың әдістерін, оның саласы модулярлық арифметиканы, пайдалану криптографияны жеке ғылым саласына айналдырды. Ал компьютерлік техниканы пайдалану компьютерлік криптография деген жаңа білім саласын туғызды.
Сонымен қатар, криптографияның нақты есептерін шешу үшін техника мен технологияның, программалық және аппараттық жабдықтардың, байланыс арналарының сапасының ролі өте жоғары. Алдыңғы тарауларда айтылғандай, ақпараттың қауіпсіздігін қамтамасыз етуде криптографияның ақпарат қорғау мүмкіншілігінің және сенімділігінің жоғары екендігі, оған негізделген әдістердің кең тарағандығы белгілі.
Криптографияның даму тарихы мен адамзаттың пайдалануын үш кезеңге бөлуге болады [1,9-11]:
1-ші кезең. Криптография ғылым саласы ретінде зерттелінбеген, бірегей жүйелік тәсілдері болмаған кезең. Бұл кезеңді ғылымға дейінгі кезең деп атайды.
2 – ші кезең. Бұл кезең ғылыми кезең деп аталады, ол К. Шеннонның «Теория связи в секретных системах» деген 1949 жылы шыққан кітабынан басталады.
3 - ші кезең. Бұл кезең заманауи кезеңі деп аталады, ол У. Диффи мен М. Хеллманның «Новые направления в криптографии» деген 1976 жылы жарық көрген кітабынан басталады. Осы кітапта қарастырылған концепцияның негізінде 1978 жылы үш математик Р. Ривест (Rivest), А. Шамир (Shamir), Л. Адлеман (Adleman) жаңа криптографиялық шифрлау әдісін ұсынды. Ол әдіс осы авторлардың фамилияларының бас әріптерінен құралған RSA деген атпен белгілі [9-11,13-16 ].
Кейбір авторлардың зерттеулерінде криптографияның даму тарихын төрт кезеңге бөледі:
1. Аңғырт криптография (XVI – ғасырдың басына дейін).
2. Формалды криптография (XV – ғасырдың соңынан - XX – ғасырдың басына дейін).
3. Ғылыми криптография (XX – ғасырдың басынан, 30-жылдардан – XX – ғасырдың 60-жылдарына дейін).
4. Компьютерлік криптография (XX – ғасырдың 70-жылдарынан бастап).
Ғылыми криптографияның пайда болуы математика ғылымының дамуымен байланысты. Ұлы ғалымдар Эйлер, Ферма, Лагранж және басқа математиктердің зерттеулерінің арқасында сандар теориясы дамып, криптографияда қолданылатын математикалық әдістер криптографияның ғылым саласына айналуға мүмкіндік берді.
Өткен ғасырдың 50-60 – жылдары пайда болған электрондық есептеу техникасының жаңа пайдалану облысы – компьютерлік криптография ғылым саласы ретінде дамыды. Бір жағынан есептеу техникасының пайда болуы компьютерлік желілер мен жүйелердің пайда болуына келтірсе, екінші жағынан компьютерлер қаскүнемдердің де жақсы құралы болды. Сондықтан кейінгі жылдары компьютерлік криптографияның дамуы аса өзекті мәселе болды. Ақпаратты қорғауға арналған әдістер дами бастады.
Қазіргі кезде ақпаратты қорғаудың әдістерін түрлерге бөлгенде криптографиялық әдістердің келесі классификациясы қарастырылады (5.2 - сурет)[1]:
| Криптографиялық әдістер |
| Шифрлау |
| Кодтау |
| Стеганография |
| Сығу |
| Ауыстыру |
| Алмастыру |
| Гаммалау |
| Түрлендіру |
| Комбинациялау |
12.2 сурет - Ақпаратты қорғаудың криптографиялық әдістерінің классификациясы
Шифрлау әдістерінің түрлері өте көп әрі олар ертеден қолданыста болып келеді. Ертеде қолданыста болған әдістердің бір түрі – шифрлануға тиісті мәтіннің таңбаларының орындарын ауыстыру әдістері.
Одан кейін пайдаланылған шифрлау әдістеріне жататыны алмастыру әдістері. Бұл әдістерде белгілі бір әліппе немесе кесте шифрлау кілті ретінде қарастырылып, шифрлануға тиісті мәтіннің таңбаларын сондағы таңбалармен алмастырылады. Шифрлау мен шифрды ашу тәсілдері келесі тарауда кеңірек қарастырылады.
Гаммалау әдісі бойынша белгілі бір арнайы тізбек қарастырылады. Шифрлануға тиісті мәтін блоктарға бөлінеді. Блоктың әрбір таңбасы арнайы тізбектің таңбаларымен қосылады. Көбінесе арнайы тізбек кездейсоқ сандардың тізбегі түрінде алынады.
Аналитикалық түрлендіру математикалық өрнектерді түрлендіру амалдарын пайдалануға негізделген. Мысалы, матрицалар мен векторларды пайдаланып, оларға қолданылатын амалдар шифрлау процесінде қолданылады. Сонымен бірге, сандарды бір жүйеден басқа жүйеге ауыстыру әдістері жиі қолданылады.
Комбинациялық әдістер бірнеше әдістерді (екі немесе одан көп) пайдалануға негізделген. Бірнеше әдістерді пайдалану криптожүйенің беріктігін арттырады.
Криптографияның идеясы мен әдістерін түсіндіру үшін келесі қарапайым жағдайлар қарастырылсын. Бірінші жағдай – пайдаланушы өзінің құпия паролін компьютерде сақтасын. Қаскүнем X компьютерден ол парольді тауып алуына мүмкіншілігі бар. Екінші жағдай – қашықта орналасқан пайдаланушы желіге кіруі үшін өзінің паролін енгізуге тиісті. Желідегі ақпаратты, оның ішінде пайдаланушының паролін қаскүнем X ұстап алатын мүмкіншілігі бар.
Осындай проблемаларды шешу үшін криптографиялық әдістер қолданылады. Ол әдістер көбінесе бір бағытты деп аталынатын функцияларды (one-way function) пайдаланумен байланысты.
Бір бағытты функция туралы түсінікті беру үшін келесі анықтамалар қарастырылсын.
1-ші анықтама. Берілген кез келген функция
y = f(x) (12.1)
тура функция деп аталынса, онда
x = f-1 (y) (12.2)
кері функция деп аталынады.
2- ші анықтама. Егер (12.1) функциясының мәнін есептеу қиындық туғызбаса, ал (12.2) функциясын есептеу үшін өте көп есептеу ресурстарын пайдалану қажет болса, онда (12.1) функциясы бір бағытты функция деп аталынады [1].
Мысал ретінде келесі функция қарастырылсын:
y = ax mod p , (12.3)
мұндағы p - қарапайым сан, 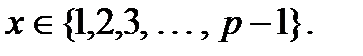
Осы функцияның кері функциясы келесі түрде жазылады:
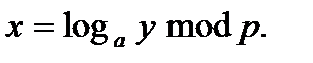 (12.4)
(12.4)
Бұл функция дискретті логарифм деп аталынады [1].
Іс жүзінде (12.3) функциясының мәнін табу қиындық туғызбайды, ал (12.4) функциясын есептеу өте күрделі. Бұл тұжырымдар туралы төменде тереңірек қарстырылатын болады.
Ақпаратты криптографиялық әдістермен құпияландыруға қойылатын негізгі талаптар:
1 Деректерді криптографиялық әдістермен құпия түрге келтірудің (жабудың) күрделілігі мен тұрақтылығы олардың көлемі мен құпиялылық деңгейіне байланысты.
2 Қаскүнемге шифрлау әдісі белгілі болған жағдайдың өзінде шифрлау сенімді болуы үшін құпиясы ашылмайтындай болуы тиіс.
3 Ақпаратты шифрлау әдісі, пайдаланылатын кілттер мен оларды тарату механизмдері өте күрделі болмауы керек.
4 Ақпаратты тура және кері түрлендірулер формалды түрде болуы керек. Ол процедуралар хабарламаның ұзындығына байланысты болмауы тиіс.
5 Түрлендіру кезінде жіберілген қате жүйеге тарамауы тиіс.
6 Қорғаныс үшін енгізілетін артықшылықтар аз болуы тиіс.
Криптографиялық әдістер келесі аса маңызды қолданбалы есептерді шешуде кең қолданылады [1]:
- электронды цифрлық қолтаңба;
- электрондық ақшалар;
- электрондық жеребе салу;
- бір мезгілде келісім шарт (контракт) жасау;
- бағалы қағаздар мен құжаттарды жалған жасау;
- электрондық дауыс беру.
Қазіргі кезде автоматтандырылған жүйелердегі ақпарат қорғауда электронды шифрлау құрылғылары пайдаланылады. Олардың көмегімен шифрлау және шифрды ашу амалдары жылдам орындалатын болады және криптоберіктікті қамтамсыз етуде жеңілдік туады. Шифрлау техникасын құрастыруда және пайдаланғанда мамандар қазіргі кездегі криптографияның жетістіктерін, математика, физика, электроника, информатика және т.б. ғылым салаларын жақсы білуі міндетті.
Дата добавления: 2016-06-02; просмотров: 4791;
