Шектің тербеліс теңдеуін Д’ Аламбер әдісімен шешу
Барлық мүмкін толқындық процестер мына теңдеумен жазылады:
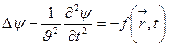
мұндағы 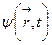 -скаляр шама (мысалы, электромагниттік өрістің скаляр потенциалы) немесе векторлық шаманың декарттық компоненті (мысалы,
-скаляр шама (мысалы, электромагниттік өрістің скаляр потенциалы) немесе векторлық шаманың декарттық компоненті (мысалы, 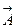 векторлық потенциалдың)
векторлық потенциалдың) 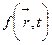 функциясы (толқындардың көзі) берілген.
функциясы (толқындардың көзі) берілген. 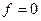 болған жағдайда бір шекті теңдеуді аламыз
болған жағдайда бір шекті теңдеуді аламыз
Шектің тербеліс теңдеуі жайындағы есепті қарастырайық. Шектің ұзындығы үлкен болғанда оның ұштарындағы шарттарды ескермеуге болады. Осындай шектің тербелісі туралы есеп
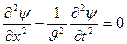 (1)
(1)
теңдеуін берілген бастапқы шарттар мен:
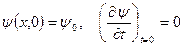 (11)
(11)
Шарттары бойынша шешуге әкеледі. Сонымен бірге 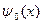 және
және 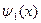 бүкіл Ох осінде анықталған. Бұл теңдеудің жалпы шешімі
бүкіл Ох осінде анықталған. Бұл теңдеудің жалпы шешімі
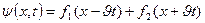 (2)
(2)
түрінде болатынын біз білеміз. Мұндағы 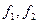 –еркімізше алынатын дифференциалдық функциялар. Олардың физикалық мағынасын анықтаймыз.
–еркімізше алынатын дифференциалдық функциялар. Олардың физикалық мағынасын анықтаймыз. 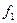 функциясы функцияның аргументі нақты белгшіленген, яғни
функциясы функцияның аргументі нақты белгшіленген, яғни 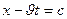 немесе
немесе 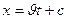 , нүктелерде ғана бірдей мәндерді қабылдайтыны анық. Бұдан шығатыны:
, нүктелерде ғана бірдей мәндерді қабылдайтыны анық. Бұдан шығатыны: 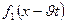 функциясы берілген мәнге ие болатын нүкте, Ох осімен оң бағытта
функциясы берілген мәнге ие болатын нүкте, Ох осімен оң бағытта 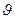 жылдамдықпен орын ауыстырады. Басқаша айтқанда,
жылдамдықпен орын ауыстырады. Басқаша айтқанда, 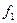 функциясы оңға қарай
функциясы оңға қарай 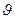 жылдамдықпен тарайтын толқынды сипаттайды. Сол сияқты
жылдамдықпен тарайтын толқынды сипаттайды. Сол сияқты 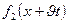 функциясы сонда(й жылдамдықпен солға қарай тарайтын толқынды сипаттайды.
функциясы сонда(й жылдамдықпен солға қарай тарайтын толқынды сипаттайды.
Жалпы жағдайда кез-келген толқын мүмкін, яғни (1) теңденудің кез-келген шешімі қарама-қарсы бағытта тарайтын екі толқынның суперпозициясы болып табылады.
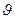 -толқынның фазалық жылдамдығы және тасымалымен байланысты емес екенін еске сақтау керек. Мысалы, қарастырылып отырған шектің тербелісі жайындағы есепте
-толқынның фазалық жылдамдығы және тасымалымен байланысты емес екенін еске сақтау керек. Мысалы, қарастырылып отырған шектің тербелісі жайындағы есепте 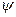 - шектің нүктелерінің көлденен ығысуы,
- шектің нүктелерінің көлденен ығысуы, 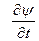 - шектің көлденен тербелістерінің жылдамдығы, сонымен бірге бұл функциялар арқылы тербелістегі шектің энергиясы (потенциалдық және кинетикалық) өрнектелелді, ал
- шектің көлденен тербелістерінің жылдамдығы, сонымен бірге бұл функциялар арқылы тербелістегі шектің энергиясы (потенциалдық және кинетикалық) өрнектелелді, ал 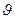 – тербелістің шектің бойымен таьралу жылдамдығы.
– тербелістің шектің бойымен таьралу жылдамдығы. 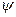 және
және 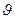 бір-бірімен байланыспаған.
бір-бірімен байланыспаған.
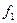 және
және 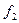 функцияларының түрлері әрбір нақты жағдайда бастапқы шарттармен анықталады.
функцияларының түрлері әрбір нақты жағдайда бастапқы шарттармен анықталады.
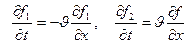
және
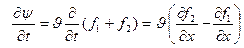
екенін ескерсек, мына теңдеуді аламыз:
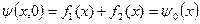 (3)
(3)
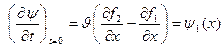
Соңғы теңдеуді интегралдаймыз:
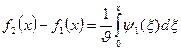 (4)
(4)
мұндағы, 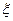 -интегралдау айнымалысы. (3) және (4) теңдеулерді қосып және азайтып,
-интегралдау айнымалысы. (3) және (4) теңдеулерді қосып және азайтып, 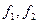 функцияларын табамыз:
функцияларын табамыз:
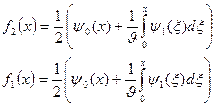
Бұл формулалардағы Х аргументін сәйкес  және
және  өрнектерімен алмастыра отырып, теңдеудің шешімін өрнектейтін функцияларды аламыз:
өрнектерімен алмастыра отырып, теңдеудің шешімін өрнектейтін функцияларды аламыз:
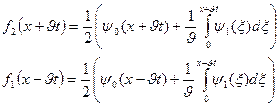
Бұл өрнкетерді (2) формулаға қойып, келесі функцияны аламыз.
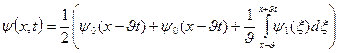
Бұл қойылған есептің шешімі. Оны Д’Аламбер шешімі деп атайды.
Дата добавления: 2016-10-17; просмотров: 1825;
