Принцип Даламбера для системы материальных точек

Рассмотрим систему 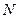материальных точек. К каждой точке системы в общем случае приложены равнодействующая активных сил и равнодействующая реакций связей. Применяя принцип Даламбера к каждой точке системы, получим

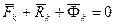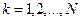, , (214)

где 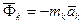– сила инерции для 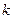-ой точки. Условия (214) можно представить в эквивалентной форме:

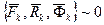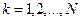, . (215)

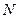векторных условий (214) или (215) выражают принцип Даламбера для системы: при движении механической системы активная сила и реакция связей вместе с силой инерции составляют равновесную систему сил для каждой точки системы.

Принцип Даламбера для системы по содержанию не отличается от уравнений движения точек системы.

Представим равнодействующую силу, приложенную к каждой точке системы, разложенной не на активную силу и реакцию связей, а на внутреннюю и внешнюю силы по отношению ко всей системе:

,

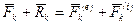Тогда принцип Даламбера для системы можно представить в другой форме:

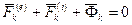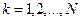, . (216)

Из принципа Даламбера для системы в форме (214) или (216) можно получить следствия в виде шести условии равновесия для сил, действующих на точки системы, и сил инерции.