Орытып шығару.

(3)-(10) теңдеулерін шешу әдістерін қарастырмас бұрын, осы теңдеулерге келетін кейбір физикалық есептерді мысалға келтірейік. Физикалық заңды сипаттайтын теңдеуді барлық жағдайда қорытып шығару мүмкін емес екенін айтакету керек. Мысалы, шектің тербеліс теңдеуін қорыту үшін Ньютонның теңдеулері қолданылады. Ал бұл теңдеудін өзін қорытып шығаруға болмайды. Ол- негізгі, бастапқы болып табылады. Максвелл және Шредингер теңдеулерін де қорытып шығару мүмкін емес. Басқаша айтқанда, негізгі физикалық заңдардың теңдеулерін табу, яғни «ашу» керек. Әрине, мұндай теңдеулер «бос жерде» пайда болмайды, яғни жаңа физикалық заңдарды іздеу оған дейінгі бар теориялар мен түсіндіру мүмкін емес көп эксперимент нәтижелерін жинақтаудан басталады. Физикалық теорияны құру экспериментке ққайшы келмейтін дұрыс теңдеулерді іздеуге әкеледі.

Енді нақты мысалдарды қарастырамыз.

1. Керілген шектің шексіз аз көлденең тербелестерінің теңдеуі.

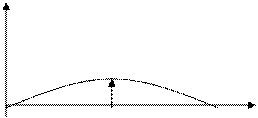
Ұзындығы l және көлденең қимасы тұрақты бір текті шек екі А мен В нүктелеріне бекетіліп, керілген болсын. Егер шекті ауытқытса, ол тепе-теңдің қалпының маңында көлденең тербелістер жасайды. Тербелісті Оху жазыктығында өтеді делік. Онда уақыт мезетіндегі нүктенің х ығысуын анықтайтын U(х, t) векторы Ох осіне перпендикуляр болады, яғни U= е_у U_у(х, t).

Т- t уақыт мезетіндегі координатасы х нүктедегі шектің керілу күші х және х+dх нүктелері арасындағы шектің элементар бөлігін қарастырайық.

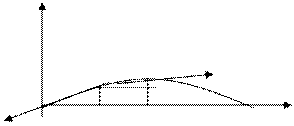Бастапқы уақыт мезетінде, шек Ох осімен сәйкес келгенде, оның ұзындығы dх. Егер dm-осы бөліктің массасы болса, Ньютонның II-заңына сәйкес

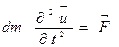(1)

Мұндағы 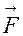-шектің алынған бөлігінің ұштарына түсірілген керілу күшініуі тең әсерлі күші (шек өте жіңішке болғандықтан ауырлық күшін ескермейміз): F=T(x)+T(x+dx)=T₁+T₂.

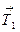және 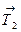керісу күштері шектің сәйкес нүктелерінде жанама бойымен бағытталған.

(1)теңдеуді координата осьтеріне проекциялап мынаны аламыз:

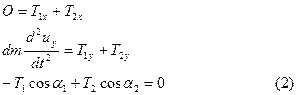
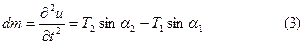
Шек шексіз аз тербелістер жасайтын жағдайда қарастырамыз. Сонымен бірг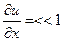е және 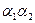бұрыштары кішкентай сондықтан қарастырылып отырған шектің бөлігінің ұзындығы өзгермейді деп есептеуге болады. Шындығында

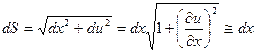
Осындай дәлдікпен 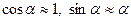. Бұл жағдайда T₁=T₂, яғни шектің керілу шамасы барлық нүктеде бірдей. Осыны ескере отырып (3) теңдеуді мына түрде жазуға болады

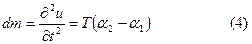
Бірақ 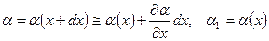cондықтан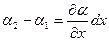

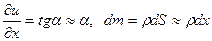
Мұндағы 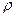-шектіу сызықтық тығыздығы. Сонда

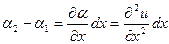
Ал (4) теңдеу былай өзгереді:

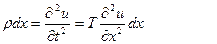
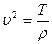белгілеуін енгізсек, ең соңында мынаны аламыз:

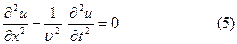
Лекция №9.