Координаттардың қисық сызықты ортогональдық жүйесі. Ламе коэффициенттері.

Өріс теориясының негізгі ұғымдарының (u(M) скаляр өрістің градиенті 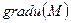, 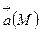векторлық өрісінің дивергенциясы 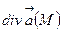және роторы 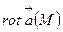) анықталған физикалық мағынасы болады және ол координаттар жүйесін таңдап алуға тәуелсіз. Бірақ нақты есептерді шығарған кезде бұл шамаларды есептеу үшін белгілі бір координаттар жүйесін қолдануға тура келеді. Кейде декарттық координаттар жүйесін қолдану қолайсыз болады. Мұндай жағдайларда нүктенің кеңістіктегі орны х,у, z декарттық координаттар жүйесімен емес, осы есеппен табиғи түрде байланысқан 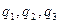сандар үштігімен анықталады. Мысалы, осьтік симметриялы есептер үшін цилиндрлік координаталарды, ал сфералық симметриялыларға-сфералық координаттарды қолданған ыңғайлы.

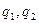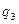Нүктенің кеңістегі орнын анықтайтын және сандары қисық сызықты координаталар деп аталады. Әр бір 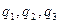қисық сызықты координаттар үштігіне кеңістіктің анықталған нүктесі сәйкес келуі керек және керісінше, кеңістіктің әрбір нүктесіне сандардың 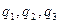үштігіне сәйкес келуі керек.

Қайсыбір нүктенің радиус-векторы оның тік бұрышты координаттарымен бір мәнді анықталатындықтан қисық сызықты координаталар осы нүктенің декарттық координаттарының функциясы болып табылады: 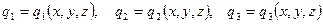және керісінше M нүктесінің тік бұрышты декарттық координаталары қисық сызықты координаталардың функциясы болады: 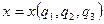, 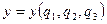және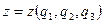

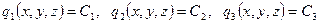теңдеулері скаляр 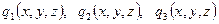функциялары үшін деңгейлік беттерді анықтайды. 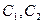және 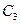тұрақтыларына әртүрлі мәндер бере отырып координаттық деп аталатын беттер жиынтығын аламыз. Мысалы, 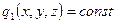координаттық бетінде 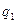координатасы тұрақты болып қалады да, тек 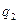және 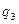координалары өзгереді. Екі координаттық беттердің қиылысуы координаталық сызық деп аталaды.

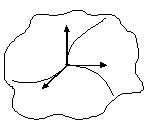
Әрбір координата сызығыынң бойымен тек бір координата өзгереді, ал қалған екеуі тұрақты болады. Координаттық сызықтардың бағыты 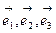бірлік базистік векторлармен (орттармен) беріледі. Олар кеңістіктің әрбір нүктесінде координаттың сызықтарына жанама бойымен ж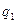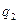әне , және 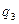айнымалыларының өсу жағына бағытталған. Тік бұрышты декарттық координаттар жүйесінде 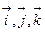орттардың бағыты кеңістіктің барлық нүктесі үшін тұрақты болып қалады, ал координаттардың қисық сызықты жүйесінде 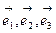бірлік вектроларының бағыттары нүктеден нүктеге өзгереді.

Қисық сызықты координаттар жүйесі ортогональді деп аталады, егер оның базистік векторлары келесі қатынастарды қанағаттандырса:

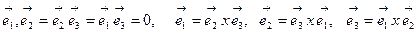(1)

Сонымен бірг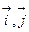е, және 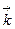–бірлік вектор болғандықтан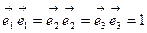

Декарттық тік бұрышты координаттар жүйесінде M нүктесінің орны 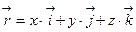радиус-векторымен, ал коорднаттардың ортогональді қисық сызықты жүйесінде – 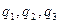қисық сызықтық координаттармен берілген болсын.

Лекция №6.