Дәріс 3. Сызықты дифференциалдық теңдеулерді жазу формасы. Беріліс функциясы.
Автоматты басқару жүйелерін сипаттау кезінде сызықты дифференциалдық теңдеулердің символикалық формасы кеңінен қолданылады.
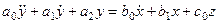(3.1)
d/dt=p, di/dti =pi түрлендірулерін қолданып (3.1) теңдеуін келесі түрде жазайық
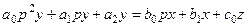(3.2)
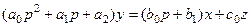(3.3)
Белгілеулер енгіземіз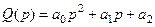 
, 
, 
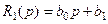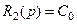. Осы белгілеулердің көмегімен (3.3) теңдеуін келесідей ықшамды түрде жазуға болады:
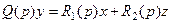. (3.4)
Q(p)-меншікті оператор
R1(p) және R2(p)-қоздыру операторлары
Беріліс функциясы. Қоздыру операторының меншікті операторға қатынасы беріліс функциясы немесе операторлық формадағы беріліс функциясы деп аталады.
(3.1) теңдеуімен немесе (3.2) — (3.4) теңдеулерімен сипатталатын буынды төмендегідей сипаттауға болады.
х кіріс шамасы бойынша W1(p) беріліс функциясы:
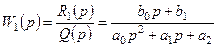(3.5)
және z кіріс шамасы бойынша W2(p) беріліс функциясы
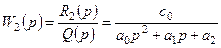(3.6)
Беріліс функциясы немесе Лаплас кескін формасындағы беріліс функциясы деп бастапқы нолдік шарттар кезінде шығыс шаманың кіріс шамаға қатынасын айтамыз.
Мысал. Лаплас кескін формасындағы беріліс функциясын табайық.
.
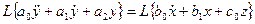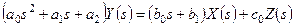, (3.8)
Мұндағы Y(s)=L{y(t)}, X(s)=L{x(t)}, Z(s)=L{z(t)}.
, 
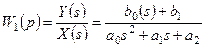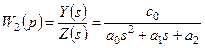. (3.9)
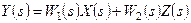. (3.10)
Сызықты дифференциалдық теңдеулердің стандартты формасы.
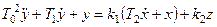, (3.11)
где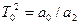 
; 
; 
; 
; 
.
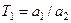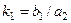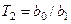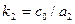Т0, T1 және T2 –уақыт тұрақтысы
k1 және k2 а коэффициенты – беріліс коэффициенттері
(3.11) келесідей жазуға болады:
.
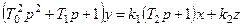Дата добавления: 2016-10-17; просмотров: 7843;