Типтік динамикалық буындар.

Жүйе құрамындағы буындардың әрқайсысына кірістік және шығыстық шамалары арасындағы байланысты бейнелейтін белгілі бір математикалық қатынастар сәйкес келеді. Егер бұл қатынастар элементар түрде болса (мысалы, дифференциалдау, тұрақты коэффициентке көбейту), онда бұл буындарды да элементар буындар деп атайды.

Бірінші және екінші ретті қарапайым дифференциал теңдеулермен өрнектелетін буындар типтік динамикалық буындар қатарына жатады. Бұл ұғымды және онымен байланысты автоматты жүйелерді талдау әдістерін 1938 жылы орыс ғалымы А.В. Михайлов ұсынған болатын.

Типтік буындарды жіктеу үшін

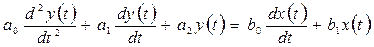(4.1)

дифференциалдық теңдеудің әртүрлі дербес нұсқаларын қарастырған жөн.

Іс жүзінде жиі кездесетін буындардың аттары және (4.1) теңдеуінің коэффициенттерінің мәндері 4.1-кестесінде келтірілген.

4.1-кесте

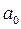
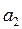
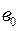
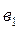
№	Буындар аты						Ескертпе
1.	Инерциясыз(пропор- ционал)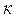
2.	1-ретті инерциялы (апериодты)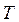
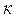
3.	2-ретті инерциялы (апериодты)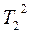
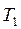
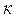
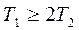
4.	2-ретті инерциялы (тербелмелі)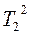
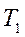
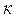
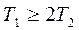
5.	Идеал интегралдаушы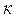
6.	Нақты интегралдаушы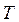
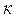
7.	Идеал дифферен-циалдаушы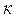
8.	Нақты дифферен-циалдаушы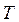
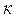
9.	Изодромды (пропорционал-интегралдауыш )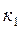
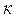
10.	Пропорционал-дифференциалдауыш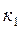
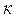
11.	Интегралдаушы қасиеті басым интегро-диффе-ренциалдауыш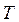
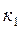
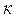
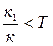
12.	Дифференциалдауыш қасиеті басым интегро-дифференциалдауыш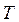

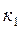
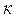
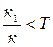
Кестедегі жалпы заңдылықтардың бір қатарын атап өтейік. Коэффициенттері 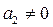және 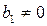буындарда статизм бар, яғни статикалық режимде олардың кірістік және шығыстық айнымалылары арасында бірмәнді байланыстықтың бар болғаны. Осы себептен бұл буындардың атына статикалық немесе позициялық сөздерін қосады. Оларға № 1, 2, 3, 4,10,11,12 буындар жатады.

Коэффициенттері 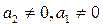және 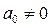буындар инерциялы деп аталынады. Оларға № 2, 3, 4, 6, 8,11,12 буындар жатады.

Тек екі коэффициенттері нөлге тең емес № 1, 5 және 7 буындар элементар немесе қарапайымдар қатарына жатады. Қалған типтік буындарды элементар буындарды тізбектеп, параллель және қарсы-параллель қосу арқылы алуға болады.

Сонымен, автоматты басқару жүйелеріне енетін буындардың құрылысы, схемалары мен физикалық әрекет принциптері әртүрлі болуы мүмкін. Бірақ орнықтылықты талдау және өтпелі процестерді есептеу тұрғысынан алып қарағанда, аталған белгілер маңызды емес екендігін және олардың әр буынының тек динамикалық қасиеттері ғана көңіл аударарлықтай болатындығын айтуға болады. Сол себепті басқару теориясында буындарды динамикалық қасиеттері бойынша жіктеу қолданылады. Автоматты реттеу жүйелерінде негізгі типтік буындарға күшейткіш (инерциясыз), апериодтық (инерциялық), интегралдауыш, дифференциалдауыш, тербелмелі буындар жатады. Ал, барлық өнеркәсіп объектілері, әдетте тасымалдық не сыйымдылық кешігумен сипатталатындықтан, сызықтық буындардың негізгі типтеріне қосымша әуелден-ақ бейсызықты болатын кешігуші буындар туралы басты ұғымды да қарастырамыз.