Раус – Гурвиц критерийі
Кейде алгебралық деп аталынатын Раус-Гурвиц критерийiнiң мәнi былайша анықталады:
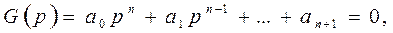
сипаттамалық теңдеудiң түбiрлерi жорамал осьтiң сол жағында жатып және жүйе орнықты болуы үшiн Гурвицтiң барлық 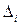 диагональ минорлары сипаттамалық теңдеудiң оң коэффициенттерi кезiнде оң болуы қажеттi әрi жеткiлiктi. Сипаттамалық теңдеуден Гурвицтiң бас анықтауышы мынаған тең:
диагональ минорлары сипаттамалық теңдеудiң оң коэффициенттерi кезiнде оң болуы қажеттi әрi жеткiлiктi. Сипаттамалық теңдеуден Гурвицтiң бас анықтауышы мынаған тең:
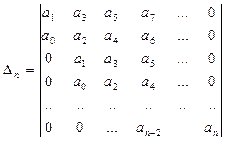 (6)
(6)
Осы анықтауышты құрғанда диагональ бойымен коэффициенттердi өспелi дәреже бойынша жазады. (6)-дағы үзiк сызықпен таңбаланған барлық диагональ минорлары ао>0 кезiнде оң болуы тиiс. Мысалы, бiрiншi реттiк жүйе үшiн
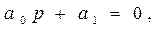 (7)
(7)
орнықтытылық шарты
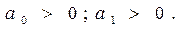
Екiншi реттi жүйе үшiн
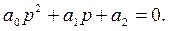 (8)
(8)
Қажеттi және жеткiлiктi шарт орындалуы үшiн сипаттамалық теңдеудiң барлық коэффициенттерi оң болуы тиiс: 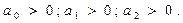
Үшiншi реттi жүйе үшiн
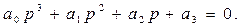 (9)
(9)
(5.9) сипаттамалық тендеуiнiң барлық коэффициенттерi, оған қоса екiншi реттi ∆2 анықтауышы оң болуы қажеттi әрi жеткiлiктi:
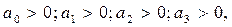 (10)
(10)
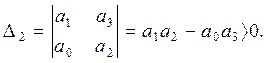 (11)
(11)
Төртiншi реттi жүйе үшін
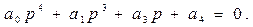 (12)
(12)
(12) сипаттамалық теңдеудiң барлық коэффициенттерi, оған қоса ∆2 және ∆3 анықтауыштары оң болуы қажеттi әрi жеткiлiктi:
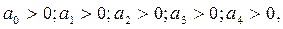
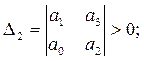
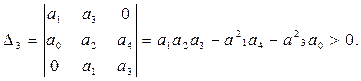 (13)
(13)
Осылайша үшiншi және төртiншi реттi теңдеулер үшiн коэффициенттердiң оң болуынан басқа (11), (13) теңсiздiктерiнiң орындалуы да қажет.
Іс жүзiнде пайдаланғанда алдымен теңдеудiң барлық коэффициенттерiнiң таңбасын тексерiп, содан кейiн ең төмендегiсiнен бастап анықтауыштарды құру керек.Егер қайсыбiр анықтауыш нөлден кiшi болса,онда келесi анықтауыштардың шамасын iздеудiң қажетi жоқ, олардың мәнi бәрiбiр терiс болады.
мысал. Гурвиц критерийi бойынша З динамикалық буыннан (үзбеден) — бiрiншi реттi екi апериодтық және бiр интегралдық буыннан тұратын астатикалық АРЖ-ның орнықтылығын тексеру керек .
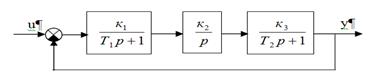
Дәріс 7. Жиіліктік орнықтылық критерийі. Аргумент принципі. Михайлов критерийінің орнықтылығы. Найквист жиіліктік критерийінің орнықтылығы.
Михайлов критерийі
Бұл критерийдi А.В. Михайлов 1938 жылы жариялаған. Ол сызықты тұйықталған автоматты реттеу жүйелерiн зерттеуге арналған. Автоматты жүйелердiң орнықтылығын анықтау жүйенiң сипаттамалық теңдеуiн талдауға негiзделген.
Михайлов годографы бойынша комллекстi айнымалы жазықтығында орналасатын қисықтың түрi бойынша жүйе орнықты ма, жоқ па екенiн анықтайды.
Михайлов қисығын салу үшiн

сипаттамалық теңдеуiндегi 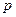 -ның орнына
-ның орнына 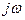 -ны қойып, келесіні аламыз:
-ны қойып, келесіні аламыз:
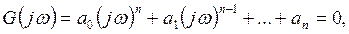
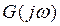 векторын нақты және жорамал бөлiктер түрiнде көрсетедi
векторын нақты және жорамал бөлiктер түрiнде көрсетедi
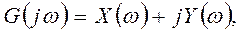
мұндағы
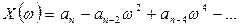
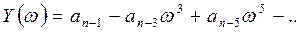
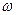 -ға 0-дан ¥ -ке дейiнгi аралықта әртүрлi мәндер бере отырып,
-ға 0-дан ¥ -ке дейiнгi аралықта әртүрлi мәндер бере отырып, 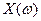 мен
мен 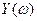 -ның бiрқатар шамасын алады, ол
-ның бiрқатар шамасын алады, ол 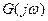 векторы ұшының координаттарын бiлдiредi. Осы нүктелердi өзара қосу арқылы Михайлов годографын аламыз. Бұл қисық
векторы ұшының координаттарын бiлдiредi. Осы нүктелердi өзара қосу арқылы Михайлов годографын аламыз. Бұл қисық 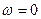 кезінде әрқашан оң нақты осъте
кезінде әрқашан оң нақты осъте 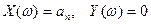 нүктесiнде басталып, ал қисық жазықтықтың
нүктесiнде басталып, ал қисық жазықтықтың 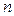 квадрантын сағат тiлiнiң бағытына қарсы бiртiндеп, координат басын баспай өтуi тиiс.
квадрантын сағат тiлiнiң бағытына қарсы бiртiндеп, координат басын баспай өтуi тиiс.
Орнықты жүйе үшiн 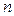 -шi квадрантта қисық шексiздiкке кетуi тиiс, өйткені тек осы жағдайда ғана (18) шарты орындалады. Сонымен Михайлов орнықтылығының критерийi былай өрнектеледi: егер
-шi квадрантта қисық шексiздiкке кетуi тиiс, өйткені тек осы жағдайда ғана (18) шарты орындалады. Сонымен Михайлов орнықтылығының критерийi былай өрнектеледi: егер 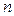 -шi реттi АРЖ орнықты болса, онда сипаттамалық вектор
-шi реттi АРЖ орнықты болса, онда сипаттамалық вектор 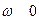 -ден
-ден 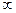 -ке дейiн өзгергенде
-ке дейiн өзгергенде 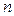
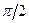 бұрышқа бұрылуы тиiс, немесе
бұрышқа бұрылуы тиiс, немесе 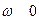 -ден
-ден 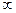 -ке дейiн өзгергенде, Михайлов годографы оң нақты жарты осьтен басталып комплекстi жазықтықтың
-ке дейiн өзгергенде, Михайлов годографы оң нақты жарты осьтен басталып комплекстi жазықтықтың 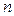 квадранттар санын сағат тiлiнің бағытына қарсы кезектеп өтуi тиiс.
квадранттар санын сағат тiлiнің бағытына қарсы кезектеп өтуi тиiс.
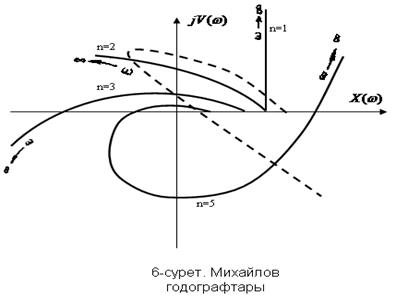
мысал. Төртiншi реттi сипаттамалық теңдеуi бар жүйенi орнықтылыққа тексеру керек
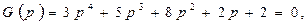
Найквист критерийі
Бұл критерийдiң жәрдемімен тұйықталмаған жүйенiң амплитудалық-фазалық-жиiлiктiк сипаттамасының түрi бойынша тұйықталған жүйенiң орнықтылығын бағалауға болады. Бұл критерий оңайлығы, көрнекiлiгi және тәжiрибе жасауға мүмкiншiлiк туғызуына байланысты іс жүзінде кең тараған.
Зерттелетін тұйықталмаған жүйенiң берiлiс функциясын бiле отырып және ондағы 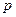 операторды
операторды 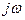 -ға алмастырып, жиiлiктiк берiлiс функциясын немесе амплитудалық - фазалық-жиiлiктiк сипаттаманы (АФС) алады. Тәжiрибе жүзiнде есептеумен алынған АФС-ның түрi бойынша жүйе орнықты ма, жоқ па, соны анықтайды.
-ға алмастырып, жиiлiктiк берiлiс функциясын немесе амплитудалық - фазалық-жиiлiктiк сипаттаманы (АФС) алады. Тәжiрибе жүзiнде есептеумен алынған АФС-ның түрi бойынша жүйе орнықты ма, жоқ па, соны анықтайды.
Орнықтылықтың Найквист критерийi былайша тұжырымдалады: егер тұйықталмаған күйдегi АРЖ орнықты болса, онда ол тұйықталған күйде де орнықты болуы үшiн тұйықталмаған жүйенiң амплитудалық-фазалық сипаттамасы координаты 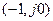 нүктенi қамтымауы қажетті әрі жеткілікті.
нүктенi қамтымауы қажетті әрі жеткілікті.
Орнықтылықтың қарастырылған тұжырымы тұйықталмаған жүйе орнықты болып, АФС теңдеуiндегi бөлшектің алымындағы полином дәрежесi бөлiмiндегi полином дәрежесiнен кем болғанда ғана дұрыс болады.
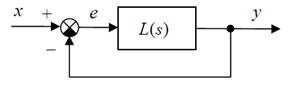
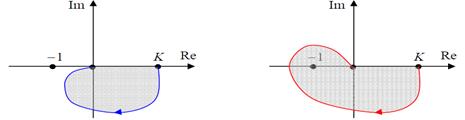
«Жүйе орнықтылық шекарасында» деген мағына жиіліктік сипаттама (−1; 0) нүктесі арқылы өтеді дегенді білдіреді.
мысал. Найквист критерийiмен статикалық АРЖ-ны орнықтылыққа тексеру қажет.
Тұйықталмаған АРЖ-ның берiлiс функциясы
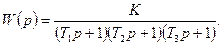
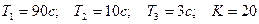 кезiнде
кезiнде 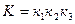 .
. 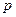 - ны‚
- ны‚ 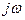 - ға алмастырып, жиілiктiк берiлiс функциясын аламыз
- ға алмастырып, жиілiктiк берiлiс функциясын аламыз
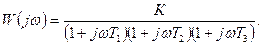
(5.25) формуладағы бөлшектiң алымы мен бөлiмін, соңғысына түйіндес комплекс санға көбейтiп оны нақты және жорамал бөлiкке ажыратсақ, мынаны шығарып аламыз:

формулаға буындардың уақыт тұрақтыларының мәндерi мен тұйықталмаған жүйенiң К күшейту коэффициентiнің мәнін қойып нақты және жорамал бөлiктерінің мәнін аламыз:
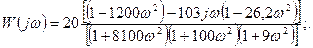
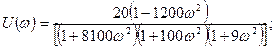
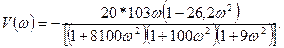
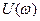 мен
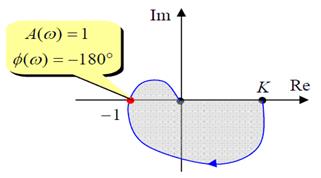
мен  -ның әртүрлi ω үшiн табылған мәндерi 5.2-кестеге енгiзiлген. 5.2-кестедегi деректер бойынша, АФС салынады (5.11-сурет). Жүйе орнықты, өйткені координаты
-ның әртүрлi ω үшiн табылған мәндерi 5.2-кестеге енгiзiлген. 5.2-кестедегi деректер бойынша, АФС салынады (5.11-сурет). Жүйе орнықты, өйткені координаты 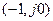 нүкте қисықтың сол жағында қалады.
нүкте қисықтың сол жағында қалады.
5.2-кесте
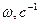
| 0,005 | 0,016 | 0,08 | 0,195 | 0,5 | ¥ | |
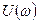
| 16,2 | 4,4 | -1,46 | -0,5 | -0,35 | ||
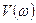
| - 8,6 | -10,4 | -1,5 | 0,03 |
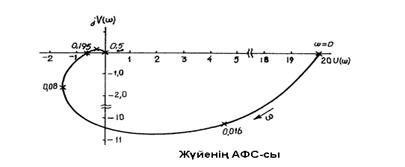
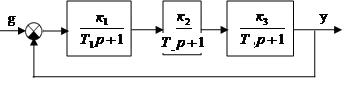
мысал.Найквист критерийiнiң жәрдемімен астатикалық АРЖ орнықтылығын тексеру керек (5.4-суреттi қараңыз).
Тұйықталмаған жүйенің берiлiс функциясы:
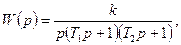
мұндағы 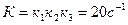 ;
; 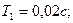
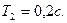 (7.27)-нен жиiлiктiк берiлiс функциясы
(7.27)-нен жиiлiктiк берiлiс функциясы 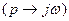
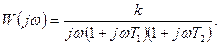
(5.28)-iн түрлендiрiп, нақты және жорамал бөлiгiн аламыз:
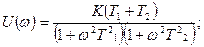
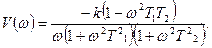
Әр түрлi жиiлiктер үшiн 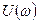 мен
мен 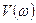 -ның мәндерi 5.3-кестеде керсетiлген.
-ның мәндерi 5.3-кестеде керсетiлген.
5.3-кесте
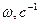
| 15,8 | ∞ | |||||
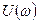
| -4,4 | -4,23 | -2,17 | -0,876 | -0,35 | -0,22 | |
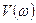
| ∞ | - 19,2 | -1,8 | -0,24 | 0,03 |
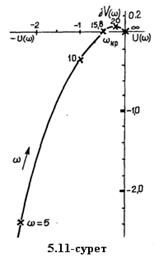 5.3-кестеден және ондағы берiлген мәндер бойынша салынған АФС (5.11-сурет) арқылы жүйенің орнықты екенiн көремiз. Қисық координаты
5.3-кестеден және ондағы берiлген мәндер бойынша салынған АФС (5.11-сурет) арқылы жүйенің орнықты екенiн көремiз. Қисық координаты 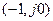 нүктенің оң жағынан өтедi. Кризистiк
нүктенің оң жағынан өтедi. Кризистiк 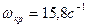 жиiлiкте комплекстi жиiлiктiк функцияның векторының модулi бiрден кiшi (0,35) болады. Интегралдаушы буынның бар болуы жүйенi астатикалық етедi. Мұндай жүйелер үшiн АФС годографы
жиiлiкте комплекстi жиiлiктiк функцияның векторының модулi бiрден кiшi (0,35) болады. Интегралдаушы буынның бар болуы жүйенi астатикалық етедi. Мұндай жүйелер үшiн АФС годографы 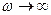 кезінде шексіздікке ұмтылуы тән.
кезінде шексіздікке ұмтылуы тән.
Дата добавления: 2016-10-17; просмотров: 5812;
