Сурет. Реттеу сапасының интегралдық бағалауын геометриялық мағыналау

6.2-мысал. Ажыратылған бірінші ретті астатизмді қадағалаушы жүйенің беріліс функциясы

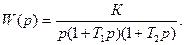
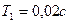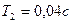Уақыт тұрақтылары және мәндеріндегі жүйенің кірісіне 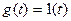бірлік сатылы әсер берілгендегі жылдамдық бойынша сапалылығын бағалау керек.

Шешімі: тұйық жүйенің беріліс функциясы

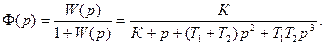
Шығыстық сигналдың Лаплас бойынша кескіні мына түрде болады:

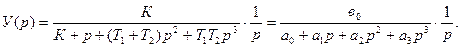
Квадраттық интегралды бағалауды табу кестесінен [5,32-тіркеме] интегралдық бағалау мәндерін анықтаймыз.

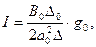
мұндағы 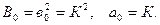Анықтауыштар мәндері

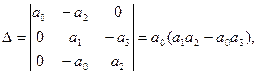
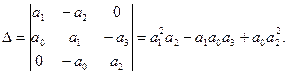
Нәтижесінде

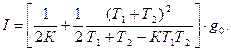
Интегралдық бағаның мәнінің минимумын алу үшін туындысын нөлге теңейміз

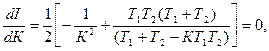
осыдан сапалылықтың оптимал мәнін аламыз:

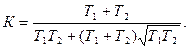
Уақыт тұрақтыларының сандық мәндерін қойғаннан кейін

Дәріс 12. Сызықты автоматты басқару жүйесінің қасиеттерін жақсарту құралдары және тәсілдері. Корректирлейтін құрылғы.

Автоматты реттеу жүйесінің құрылымдық схемасы берілген делік (7.17-сурет).

Бұл жүйенің 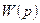беріліс функциясын мына түрде аламыз:

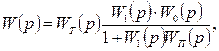(7.54)

мұндағы 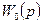мен 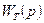– екі тізбектеле қосылған бөліктерден тұратын объектінің немесе жүйенің өзгермейтін бөлігінің беріліс функциялары;

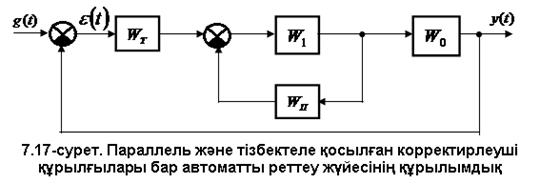
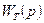– тізбектеле қосылған корректирлеуші құрылғының беріліс функциясы;

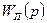– объектінің 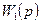беріліс функциясы бар бөлігін қамтып тұрған параллель корректирлеуші буынның беріліс функциясы.

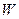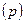Енді жүйенің қалаулы _қ және 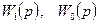беріліс функциялары аналитикалық өрнектер немесе оларға сәйкес жиіліктік сипаттамалар түрінде берілген делік.

Мақсат

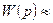
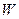_қ 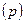(7.55)

теңдігін қамтамасыз ететін, параллель және тізбектеп жалғанған корректирлеуші құрылғылардың 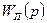, 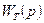беріліс функцияларын және олардың параметрлерінің сандық мәндерін анықтау.

Корректирлеу құрылғысының синтезін П.Л. Чебышевтың жалпы есебін қолдану арқылы жүргізуге болады. Ол есепті былай түсіндіруге болады. Айнымалы 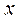мәндері үшін тұйық, яғни ақырлы 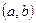интервалы және оның ішінде жатқан 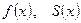екі нақты үзіліссіз функциялар берілген делік.

Өрнек құрамыз

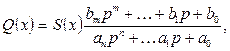(7.56)

мұндағы 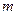мен 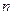берілген.

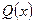функциясының 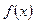функциясынан ауытқуы ең кіші болатындай 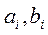нақты параметрлерді де анықтау қажет, яғни

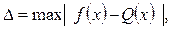
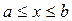болғанда.

Чебышев П.Л. есебін қолдана отыра, корректирлеуші құрылғылар синтезін жүргізейік. Ол үшін, 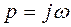болғандағы ажыратылған жүйенің қалаулы беріліс функциясы модулінің квадратын табамыз

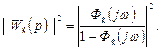(7.57)

Нәтижесінде, -ның нақты жұп бөлшек-рационалды функциясын аламыз. Енді, 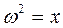деп алып, бұл функцияны 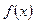деп белгілеп,

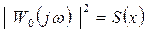және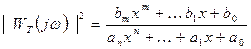

белгілеуін енгізсек, онда 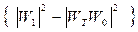айырымының абсолют мәнінің минимумын қажет ететін, корректирлеуші құрылғының синтезінің, жоғарыда келтірілген Чебышев есебіне келетінін көреміз.

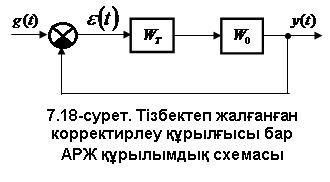Тізбектеп жалғанған кор-ректирлеуші құрылғының синте-зін қарастырайық (7.18-сурет).

Мақсат - тізбектеп жал-ғанған корректирлеуші құрыл-ғының түрімен параметрлерін анықтау.

Есепті шығару үшін (7.54) өрнегін пайдаланайық. Одан мынаны аламыз:

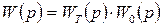(7.58)

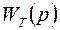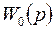және беріліс функцияларының екеуі де минимал –фазалы делік, яғни

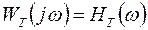
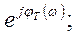
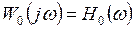
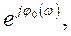
онда

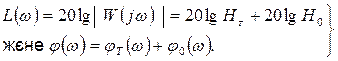(7.59)

Алынған (7.59) өрнектен, жүйенің логарифмдік 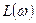амплитудалық жиіліктік және 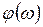фазалық жиіліктік сипаттамаларының, объекті мен тізбектеп жалғанған корректирлеуші құрылғының сәйкес логарифмдік амплитудалық 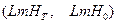жиіліктік және фазалық 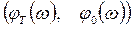жиіліктік сипаттамаларының қосындысымен анықталатындығын көреміз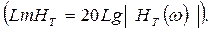

Енді параллель жалғанған корректирлеу құрылғысының беріліс функциясын табу жолын келтірейік:

1. берілген бөліктің 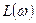логарифмдік амплитудалық сипаттамасын тұрғызамыз;

2. бүкіл жүйенің 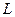_қ 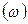қалаулы логарифмдік сипаттамасын тұрғызамыз;

3. елеулі жиіліктер 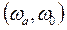интервалын анықтап,

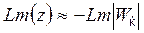
теңдігі орындалатындай етіп, бұл интервалдан 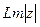сипаттамасын таңдап аламыз;

4. 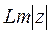сипаттамасын тұрғызамыз;

5. Жиіліктің 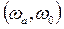интервалында

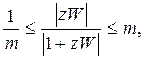(7.70)

мұндағы 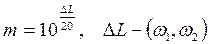жиіліктер интервалында 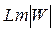сипаттамасының 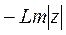сипаттамасынан айырмасы, теңсіздігін қанағаттандыратын 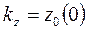мәнін таңдап аламыз;

6. Параллель корректирлеу құрылғысының синтезін таңдалынған 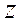беріліс функциясы бойынша, тізбектеп жалғанған корректирлеу құрылғының синтезі секілді жолмен әрі қарай жүргіземіз;

7. Корректирлеу құрылғысының күшейту коэффициентін, жүйенің күшейту коэффициенті талапқа сай болатындай етіп аламыз;

8. 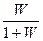функциясына сәйкес логарифмдік сипаттаманың түрін анықтаймыз; ол үшін 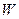және 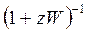функцияларына сәйкес логарифмдік сипаттамалардың ординаттарын бір-біріне қосындылаймыз;

9. Берілген сапаны қанағаттандыру шарттарының орындалуын тексереміз.

Енді құрылымдық схеманың 7.17-суреттегідей жалпы қосылысын қарастырайық . Мұнда корректирлеуші құрылғылар тізбектеле және параллель жалғанған. Жүйенің беріліс функциясынан

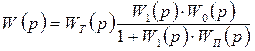(7.71)

оған сәйкес логарифмдік амплитудалық сипаттаманы алуға болады:

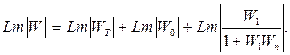(7.72)

Синтез жүргізудегі алғашқы қадам, жоғарыда келтірілгендей, берілген сапа және объект сипаттамасына қойылатын шарттарға сәйкес, қалаулы логарифмдік сипаттаманы таңдаудан басталады; ал әрі қарай, мысалы төмендегідей жүргізілуі мүмкін.

Мысалы,

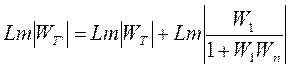(7.73)

делік, онда (7.72) өрнегінің орнына мынаны жазуға болады

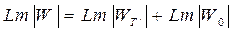. (7.74)

Бұл өрнек (7.59) формуласымен бірдей. Сондықтан 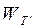беріліс функциясының синтезін, тізбектеп жалғанған корректирлеу құрылғысының синтезіндей етіп жүргізуге болады. 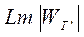анықтап, қолдағы бар төртполюстік негізінде 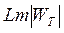таңдап алып, 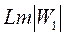біле отыра, (7.73) өрнегінен сәйкес сипаттамаларды азайта отыра, логарифмдік амплитудалық сипаттаманы

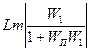(7.75)

табуға болады. Егер (7.75) сипаттама белгілі болса, онда 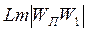сипаттама, яғни, ізделетін 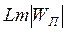логарифмдік амплитудалық сипаттама да оңай анықталады.

Егер барлық елеулі жиіліктер интервалында

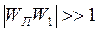(7.76)

шарты орындалатын болса, онда (10.42) формуласы

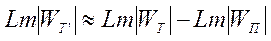(7.77)

түріне келеді және бұл жағдайдағы синтездеу тәсілінің тізбектеп жалғасқан корректирлеуші құрылғының синтезінен ешқандай айырымы жоқ.

Жалпы, тізбектеп жалғанған корректирлеу құрылғысы кәдімгі пассивті -контуры арқылы іске асырылатындығымен ерекшелінеді. Оның кемшілігін төмендегідей сипаттауға болады:

1. Жүйенің жалпы күшейту коэффициентін азайтады;

2. Дифференциалдауыш контурлардың жиіліктің кең ауқымын қамтып жатуына байланысты, бөгетке сезімталдылығы көбейеді;

3. Корректирлеуші құрылғының тиімділігі, жүйе элементтерінің сипаттамаларының орнықтылығына тәуелді;

4. Корректирлеуші құрылғы ретінде пайдаланылатын интегралдаушы буындарда рабайсыз конденсаторлар қолданылады. Параллель корректирлеуші құрылғысы бар жүйенің артықшылықтары: