Сурет. Асимптоталық ЛАС
5.4-кесте мәлiметтерiне қарай 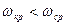 екенiн, оған қоса кризистiк жиілікте амллитуда бiрден үлкен
екенiн, оған қоса кризистiк жиілікте амллитуда бiрден үлкен 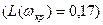 болатындығын байқаймыз, демек жүйе орнықсыз.
болатындығын байқаймыз, демек жүйе орнықсыз.
Дәріс 9. Жүйенің жазықтық параметрлерінде орнықтылық облысын тұрғызу. D-бөліктеу түсінігі. Екі параметр бойынша D-бөліктеу. Сызықты жүйелерді реттеу сапасы.
Жоғарыда қарастырылған критерийлерді жүйенің орнықтылығы жөнінде жорамал жасау үшін АРЖ барлық параметрлері берілген кезде ғана пайдалануға болады. Іс жүзінде жүйенің тек қана орнықтылығын емес, реттеу сапасын жоғарылату мақсатында оның параметрлерін белгілі бір шек аралығында өзгертіп отыру қажеттігі жиі кездеседі. Өзгертуді қажет ететін бұл параметрлер ретінде жүйе элементтерінің беріліс коэффициенттері және уақыт тұрақтылықтарымен бірмәнді байланысты сипаттаушы теңдеудің коэффициенттері қарастырылады. Сипаттаушы теңдеу коэффициенттері өзгермелі болған жағдайда жүйенің орнықтылығын анықтау үшін критерийлерді жеке-жеке пайдалану көптеген ыңғайсыздықтар туғызады. Мысалы, егер Михайлов критерийі бойынша орнықтылық аймағын анықтар болсақ, айнымалы параметрлердің әрбір мәндеріне сәйкес годографтар тұрғызуға тура келер еді, ал Гурвиц критерийін қолданар болсақ, өте күрделі де рабайсыз теңдеулерді шешу керек болар еді. Сондықтан орнықтылық аймағын айқындайтын арнайы әдістерді қолдану өте ыңғайлы. Осындай әдістердің ішіндегі, орнықтылық аймағын анықтау үшін барлық критерийлерді бір көзқараста біріктіретін, Ю.И. Неймарк ұсынған Д-бөліктеу әдісін қарастырамыз.
Тұйықталған жүйенің сипаттаушы теңдеуі
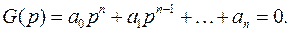 (5.32)
(5.32)
 Бұл теңдеуді нөлге айналдыратын
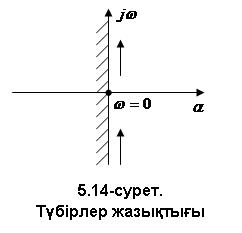
Бұл теңдеуді нөлге айналдыратын 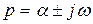 мәні орнықтылық шекарасын анықтайды. Жорамал осьтің сол жағындағы жартылай жазықтықта жатқан теңдеу түбірлері жүйенің орнықтылығына сәйкес келеді. Егер түйіндес түбірлердің ең болмағанда бір пары жорамал ось бойында жатса, онда жүйе орнықтылық шекарасында тұр. Яғни,
мәні орнықтылық шекарасын анықтайды. Жорамал осьтің сол жағындағы жартылай жазықтықта жатқан теңдеу түбірлері жүйенің орнықтылығына сәйкес келеді. Егер түйіндес түбірлердің ең болмағанда бір пары жорамал ось бойында жатса, онда жүйе орнықтылық шекарасында тұр. Яғни, 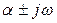 координатында орнықтылық аймағы
координатында орнықтылық аймағы 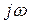 осінің сол жағында жатады, ал бұл координат жүйесінде
осінің сол жағында жатады, ал бұл координат жүйесінде 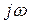 осін сол жағынан штрихтеу келісілген (ось бойымен -¥ -тен +¥ -ке қарай жылжығанда).
осін сол жағынан штрихтеу келісілген (ось бойымен -¥ -тен +¥ -ке қарай жылжығанда).
Енді (5.32) сипаттаушы теңдеудің 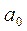 және
және 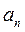 коэффициенттерінен басқалары анықталған болсын.
коэффициенттерінен басқалары анықталған болсын. 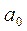 және
және 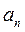 коэффициенттерінің берілген бір мәндерінде (5.32) теңдіктің түбірлер жазықтығындағы жорамал осьтің сол жағында
коэффициенттерінің берілген бір мәндерінде (5.32) теңдіктің түбірлер жазықтығындағы жорамал осьтің сол жағында 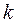 , оң жағында
, оң жағында 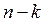 түбірлері бар. Ал
түбірлері бар. Ал 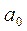 және
және 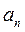 коэффициенттері мәндерінің белгілі бір ауқымда өзгерулері жорамал осьтің екі жағында жатқан түбірлер санына әсерін тигізбейді. Осы себептен
коэффициенттері мәндерінің белгілі бір ауқымда өзгерулері жорамал осьтің екі жағында жатқан түбірлер санына әсерін тигізбейді. Осы себептен 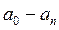 жазықтығында әрбір нүктесі (5.32) теңдеудің шешімі бола алатындай аймақты бөліп алуға болады. Бұл аймақтың әрбір нүктесіндегі
жазықтығында әрбір нүктесі (5.32) теңдеудің шешімі бола алатындай аймақты бөліп алуға болады. Бұл аймақтың әрбір нүктесіндегі 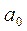 мен
мен 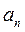 коэффициенттерінің мәндері үшін жорамал осьтің сол жағында
коэффициенттерінің мәндері үшін жорамал осьтің сол жағында 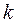 , ал оң жағында
, ал оң жағында 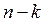 түбірлер саны орналасады. Бұл аймақты
түбірлер саны орналасады. Бұл аймақты 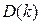 деп белгілейік. Осылайша (5.32) теңдеудің кез-келген екі коэффициенттері белгісіз, ал қалғандары берілген сандар болатын түбірлер жазықтығын
деп белгілейік. Осылайша (5.32) теңдеудің кез-келген екі коэффициенттері белгісіз, ал қалғандары берілген сандар болатын түбірлер жазықтығын 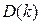 аймақтарына бөліп тастауға болады. Ал,
аймақтарына бөліп тастауға болады. Ал, 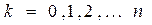 тұтас сандар бола алатындықтан, коэффициенттер жазықтығында
тұтас сандар бола алатындықтан, коэффициенттер жазықтығында 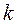 - ның әрбір мәндеріне сәйкес келетін аймақтарды көрсетуге болады. Мысалы
- ның әрбір мәндеріне сәйкес келетін аймақтарды көрсетуге болады. Мысалы 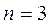 үшінші ретті теңдеуді алсақ, онда жалпы жағдайда
үшінші ретті теңдеуді алсақ, онда жалпы жағдайда 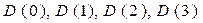 аймақтарды бөліп алуға болады. Коэффициенттер кеңістігінде
аймақтарды бөліп алуға болады. Коэффициенттер кеңістігінде 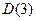 аймағы орнықтылық аймағы болады. Егер осы айтылған жағдайда сипаттамалық теңдеудің теріс таңбалы нақты бөліктері бар үш түбірі болмаса (яғни жорамал осьтің сол жағында жатқан үш түбірі) бұл жүйенің
аймағы орнықтылық аймағы болады. Егер осы айтылған жағдайда сипаттамалық теңдеудің теріс таңбалы нақты бөліктері бар үш түбірі болмаса (яғни жорамал осьтің сол жағында жатқан үш түбірі) бұл жүйенің 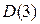 аймағы да болмайды, сондықтан жүйе орнықсыз.
аймағы да болмайды, сондықтан жүйе орнықсыз.
Егер (5.32) теңдеудің 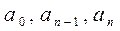 үш коэффициенттері белгісіз болса, онда
үш коэффициенттері белгісіз болса, онда 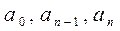 үш осьті үш өлшемдік кеңістікті қарастыратын болар едік, ал
үш осьті үш өлшемдік кеңістікті қарастыратын болар едік, ал 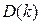 орнықтылық аймағы қайсыбір бет түрінде кескінделер еді. Белгісіз коэффициенттері көбейген сайын
орнықтылық аймағы қайсыбір бет түрінде кескінделер еді. Белгісіз коэффициенттері көбейген сайын 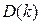 орнықтылық аймағы да көп өлшемді кеңістікке сәйкес гипербет түрінде кескінделеді. Коэффициенттер кеңістігін осылай бөліктеуді
орнықтылық аймағы да көп өлшемді кеңістікке сәйкес гипербет түрінде кескінделеді. Коэффициенттер кеңістігін осылай бөліктеуді 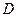 - бөліктеу деп атайды.
- бөліктеу деп атайды.
Енді (5.32) полиномның 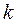 -түбірлері жорамал осьтің сол жағында жатыр делік. Теңдеудің
-түбірлері жорамал осьтің сол жағында жатыр делік. Теңдеудің 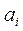 коэффициенттерінің мәндерін біртіндеп өзгерткенде түбірлер оң жақ жартылай жазықтыққа өтулері ықтимал. Бұл өту не жорамал ось арқылы, не шексіздік арқылы болуы мүмкін, және де тек теңдеу параметрлерінің
коэффициенттерінің мәндерін біртіндеп өзгерткенде түбірлер оң жақ жартылай жазықтыққа өтулері ықтимал. Бұл өту не жорамал ось арқылы, не шексіздік арқылы болуы мүмкін, және де тек теңдеу параметрлерінің 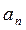 коэффициентін нөлге айналдырар мәндерінде ғана түбір нөлге тең болады. Коэффициенттер кеңістігіндегі
коэффициентін нөлге айналдырар мәндерінде ғана түбір нөлге тең болады. Коэффициенттер кеңістігіндегі 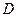 - бөліктеу аймағының шектелу қисығынан өту, түбірлердің түбірлер жазықтығында жорамал ось арқылы өтуіне сәйкес. Яғни,
- бөліктеу аймағының шектелу қисығынан өту, түбірлердің түбірлер жазықтығында жорамал ось арқылы өтуіне сәйкес. Яғни, 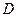 - бөліктеудің шектелу (шекаралық) қисығын (5.32) полиномдағы
- бөліктеудің шектелу (шекаралық) қисығын (5.32) полиномдағы 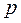 параметрін
параметрін 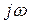 шамасына ауыстырып,
шамасына ауыстырып, 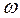 жиілікті -¥-тен +¥-ке дейін өзгерту арқылы тұрғызады. Бұл тұрғыда
жиілікті -¥-тен +¥-ке дейін өзгерту арқылы тұрғызады. Бұл тұрғыда 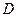 - бөліктеу шекарасын, түбірлер жазықтығындағы жорамал осьтің, сипаттаушы теңдеу коэффициенттері жазықтығындағы бейнесі ретінде қарастыруға болады.
- бөліктеу шекарасын, түбірлер жазықтығындағы жорамал осьтің, сипаттаушы теңдеу коэффициенттері жазықтығындағы бейнесі ретінде қарастыруға болады.
Сонымен, параметрлер немесе коэффициенттер кеңістігінде түбірлердің әртүрлі үлестірілу аймақтарын тұрғызу процесін 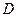 - бөліктеу, ал бұл аймақтардың шектелу сызығын
- бөліктеу, ал бұл аймақтардың шектелу сызығын 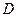 - бөліктеу қисығы деп атайды.
- бөліктеу қисығы деп атайды.
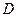 -бөліктеу әдісін бір параметрлі жазықтықта орнықтылық аймағын тұрғызу үшін қолданайық. (5.32) теңдеудің
-бөліктеу әдісін бір параметрлі жазықтықта орнықтылық аймағын тұрғызу үшін қолданайық. (5.32) теңдеудің 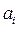 коэффициенттеріне
коэффициенттеріне 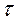 параметрі сызықты әсер етеді делік. Онда бұл теңдеуді
параметрі сызықты әсер етеді делік. Онда бұл теңдеуді 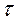 -ға сәйкес шешіп мынандай теңдеуді алуға болады:
-ға сәйкес шешіп мынандай теңдеуді алуға болады:
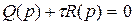 (5.33)
(5.33)
немесе
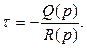
Мысалы: 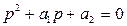 және
және 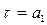 өрнегі үшін
өрнегі үшін 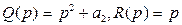 аламыз; ал
аламыз; ал 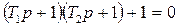 және
және 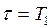 өрнегі үшін:
өрнегі үшін: 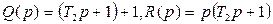 аламыз.
аламыз.
Бізге жалпы 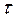 -дың нақты мәні керек. Әйтсе де уақытша
-дың нақты мәні керек. Әйтсе де уақытша 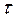 комплексті сан деп есептеп, түбірлер жазықтығындағы жорамал осьті
комплексті сан деп есептеп, түбірлер жазықтығындағы жорамал осьті 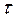 жазықтығымен кескіндейік. Бұл жазықтықтағы орнықтылық аймағын бөліп алғаннан кейін,
жазықтығымен кескіндейік. Бұл жазықтықтағы орнықтылық аймағын бөліп алғаннан кейін, 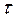 параметрінің тек нақты мәндерін қарастыруға болады.
параметрінің тек нақты мәндерін қарастыруға болады.
(5.33) теңдеуіне 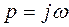 мәнін қойып және алынған теңдеуді
мәнін қойып және алынған теңдеуді 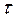 параметріне сәйкес шешіп мына өрнекті аламыз:
параметріне сәйкес шешіп мына өрнекті аламыз:
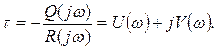 (5.34)
(5.34)
Енді 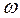 айнымалысын -¥-тен +¥ аралығында өзгерте отыра,
айнымалысын -¥-тен +¥ аралығында өзгерте отыра, 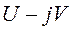 координаталар жүйесінде
координаталар жүйесінде 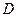 - бөліктеу қисығын салуға болады (5.15-сурет).
- бөліктеу қисығын салуға болады (5.15-сурет). 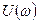
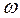 айнымалысының жұп, ал
айнымалысының жұп, ал 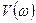 - тақ функциясы болатындығынан,
- тақ функциясы болатындығынан, 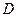 -бөліктеу қисығы әрқашан
-бөліктеу қисығы әрқашан 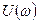 нақты оське сәйкес симметриялы болып орналасады. Сол себептен орнықтылық аймағын
нақты оське сәйкес симметриялы болып орналасады. Сол себептен орнықтылық аймағын
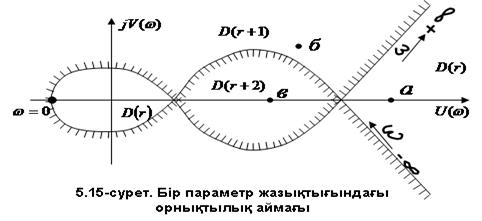
тұрғызар кезде 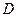 - бөліктеу қисығының жиіліктің
- бөліктеу қисығының жиіліктің 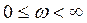 мәндеріне сәйкес бір тармағын салып алып, екінші тармағын біріншіге айналық шағылуы түрінде салса жеткілікті.
мәндеріне сәйкес бір тармағын салып алып, екінші тармағын біріншіге айналық шағылуы түрінде салса жеткілікті.
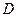 -бөліктеу қисығы
-бөліктеу қисығы 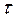 параметрі жазықтығын, түбірлердің әр түрлі орналасуына сәйкес бірнеше аймақтарға бөледі. Олардың ішінен
параметрі жазықтығын, түбірлердің әр түрлі орналасуына сәйкес бірнеше аймақтарға бөледі. Олардың ішінен 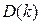 орнықтылық аймағын штрихтеу көмегімен айқындауға болады. Штрихтеу ережесі
орнықтылық аймағын штрихтеу көмегімен айқындауға болады. Штрихтеу ережесі 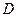 -бөліктеу қисығының түбірлер жазықтығындағы жорамал осьтің бейнесі екендігіне негізделген. Осыған сәйкес
-бөліктеу қисығының түбірлер жазықтығындағы жорамал осьтің бейнесі екендігіне негізделген. Осыған сәйкес 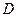 - бөліктеу қисығының бойымен
- бөліктеу қисығының бойымен 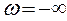 нүктесінен
нүктесінен 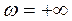 нүктесіне қарай жылжығанда орнықтылық аймағы әруақытта сол жақта жатады. Сонымен
нүктесіне қарай жылжығанда орнықтылық аймағы әруақытта сол жақта жатады. Сонымен 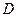 -бөліктеу қисығын
-бөліктеу қисығын 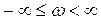 өзгергенде сол жағынан штрихтейді.
өзгергенде сол жағынан штрихтейді.
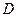 -бөліктеу қисығын штрихтелген жағынан штрихтелмеген жағына қарай бір рет кесіп өту, түбірлер жазықтығындағы жорамал ось арқылы, бір түбірдің сол жартылай жазықтықтан оң жартылай жазықтыққа өтуімен пара-пар.
-бөліктеу қисығын штрихтелген жағынан штрихтелмеген жағына қарай бір рет кесіп өту, түбірлер жазықтығындағы жорамал ось арқылы, бір түбірдің сол жартылай жазықтықтан оң жартылай жазықтыққа өтуімен пара-пар.
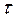 жазықтығындағы
жазықтығындағы 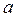 нүктесін қарастырайық (5.15-сурет). Бұл нүктеде,
нүктесін қарастырайық (5.15-сурет). Бұл нүктеде, 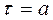 , теңдеудің сол жақ жартылай жазықтықта
, теңдеудің сол жақ жартылай жазықтықта 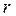 түбірі, оң жақ жартылай жазықтықта
түбірі, оң жақ жартылай жазықтықта 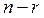 түбірі бар делік. Әзірше
түбірі бар делік. Әзірше 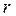 белгісіз сан. Яғни
белгісіз сан. Яғни 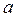 нүктесі
нүктесі 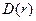 аймағында жатыр.
аймағында жатыр. 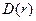 аймағы,
аймағы, 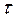 жазықтығындағы
жазықтығындағы 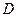 -бөліктеу қисығын кесіп өтпей-ақ
-бөліктеу қисығын кесіп өтпей-ақ 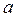 нүктесінен жете алатын, нүктелер жиынтығынан тұрады. Енді
нүктесінен жете алатын, нүктелер жиынтығынан тұрады. Енді 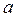 нүктесінен б нүктесіне жету үшін
нүктесінен б нүктесіне жету үшін 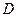 -бөліктеу қисығын штрихтелмеген жағынан штрихтелген жағына қарай бір рет кесіп өтеміз, бұл жорамал осьті түбірдің оң жақтан сол жаққа кесіп өтуімен бірдей.
-бөліктеу қисығын штрихтелмеген жағынан штрихтелген жағына қарай бір рет кесіп өтеміз, бұл жорамал осьті түбірдің оң жақтан сол жаққа кесіп өтуімен бірдей.
Яғни б нүктесі 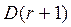 аймағында жатыр. Бұл аймақта
аймағында жатыр. Бұл аймақта 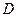 -бөліктеу қисығын кесіп өтпей-ақ жететін ,
-бөліктеу қисығын кесіп өтпей-ақ жететін , 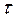 жазықтығының басқа да нүктелері жатыр. Осылай пайымдау арқылы в нүктесінің
жазықтығының басқа да нүктелері жатыр. Осылай пайымдау арқылы в нүктесінің 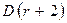 аймағында жатқанын анықтауға болады. Жазықтықты аймақтарға бөліп алғаннан кейін, орнықтылыққа «үміткер» аймақты табады. Ол
аймағында жатқанын анықтауға болады. Жазықтықты аймақтарға бөліп алғаннан кейін, орнықтылыққа «үміткер» аймақты табады. Ол 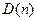 ең үлкен белгілік саны бар аймақ (
ең үлкен белгілік саны бар аймақ ( 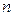 теңдеудің реті болғандықтан одан үлкен белгілі сан жоқ).
теңдеудің реті болғандықтан одан үлкен белгілі сан жоқ).
мысал.Уақыт тұрақтылары  және
және 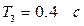 апериодтық үш буыннан тұратын жүйенің орнықтылық аймағын
апериодтық үш буыннан тұратын жүйенің орнықтылық аймағын 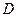 - бөліктеу әдісімен тұрғызу қажет. Орнықтылық аймағын жалпы
- бөліктеу әдісімен тұрғызу қажет. Орнықтылық аймағын жалпы 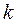 беріліс коэффициенті жазықтығында саламыз.
беріліс коэффициенті жазықтығында саламыз.
Жүйенің сипаттауыш теңдеуі
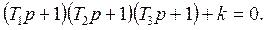
Теңдеудегі 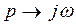 алмастырып, оны
алмастырып, оны 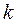 - ға сәйкес шешеміз:
- ға сәйкес шешеміз:
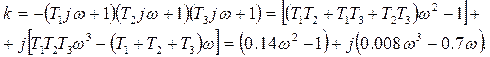
Жиілік 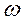 мәндерін 0-ден ¥-ке дейін өзгерте отыра,
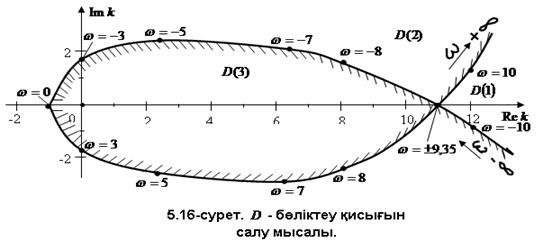
мәндерін 0-ден ¥-ке дейін өзгерте отыра, 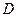 - бөліктеу қисығын тұрғызамыз (5.16-сурет). Штрихтеу және түбірлердің өтуі жөнінде пайымдау бойынша
- бөліктеу қисығын тұрғызамыз (5.16-сурет). Штрихтеу және түбірлердің өтуі жөнінде пайымдау бойынша 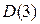 аймағының орнықтылық аймағы екенін дәлелдеу қиын емес. Шынында да,
аймағының орнықтылық аймағы екенін дәлелдеу қиын емес. Шынында да, 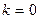 болғанда сипаттаушы теңдеудің үш түбірі де теріс таңбалы:
болғанда сипаттаушы теңдеудің үш түбірі де теріс таңбалы:
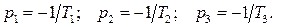
Дәріс 10. Автоматты басқару жүйесінің сапа көрсеткіштері. Баға сапасын реттеудің түбірлік әдістері.
Автоматты реттеу жүйесiнің қозғалыс орнықтылығы оның негізгi, бiрақ жеткiлiктi емес қасиетi болып табылады. Автоматты реттеу жүйесiнiң қозғалыс орнықтылығы немесе орнықсыздығы деп ондағы өтпелi процестiң өшуінің бар не жоқ екендiгiнен түсiнуге болады.
Реттеу процесiнің сапасы ретiнде автоматты реттеуіштiң жеткiлiктi дәлдiкпен реттелетiн параметрдiң шамасын белгiленген өзгерiс заңы бойынша ұстап отыру қабiлетiн айтуға болады. Реттеу процесiнің сапасы реттелетін параметр белгiленген шамадан аз ауытқыса, әрi белгiленген режимге тез жетсе, соғұрлым жоғары болады.
Сапаның негiзгi көрсеткiштерiне: реттеу мерзiмi, асыра реттеу, тербелмелi және қалыптасқан статикалық ауытқу жатады. Оған қоса, нақты жағдайда реттеу сапасына басқа да талаптар қойылады, айталық, реттелетiн шаманың өзгерiсiнiң ең үлкен жылдамдығы, оның тербелiсiнiң негiзгi жиiлiгi т.б. 6.1-суреттегiдей 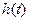 өтпелi функция мысалында реттеу сапасының негiзгi көрсеткiштерiн қарастырайық.
өтпелi функция мысалында реттеу сапасының негiзгi көрсеткiштерiн қарастырайық.
 |
Реттеу мерзiмi
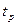 абсолют шама
абсолют шама 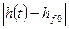 -ның жүйе жұмысының
-ның жүйе жұмысының 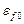 берiлген дәлдiгiнiң ауқымынан аспайтын деңгейге жеткенiне дейiнгi уақыт аралығы.
берiлген дәлдiгiнiң ауқымынан аспайтын деңгейге жеткенiне дейiнгi уақыт аралығы.
Іс жүзiнде 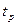 реттеу мерзiмі деп, өтпелi қате абсолют шамасының әлi де мүмкiндiк мәнiнен (әдетте, ол реттелетін параметрдiң қалыптасқан мәнінің З-5%-ін құрайды) кем болатын уақыт аралығын (өтпелi процестің басынан) айтады. 0-ден
реттеу мерзiмі деп, өтпелi қате абсолют шамасының әлi де мүмкiндiк мәнiнен (әдетте, ол реттелетін параметрдiң қалыптасқан мәнінің З-5%-ін құрайды) кем болатын уақыт аралығын (өтпелi процестің басынан) айтады. 0-ден 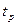 - ға дейiнгi уақыт аралығы реттеу мерзiмі болып табылады. Реттеу мерзiмi өтпелi процестiң ұзақтығын анықтайды.
- ға дейiнгi уақыт аралығы реттеу мерзiмі болып табылады. Реттеу мерзiмi өтпелi процестiң ұзақтығын анықтайды.
Асыра реттеу 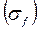 деп реттелетін шаманың процентпен өрнектелген қалыптасқан мәнiнен
деп реттелетін шаманың процентпен өрнектелген қалыптасқан мәнiнен 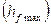 максимал ауытқуын
максимал ауытқуын 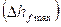 айтады.
айтады. 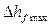 абсолют шама өтпелi сипаттамадан анықталады:
абсолют шама өтпелi сипаттамадан анықталады:
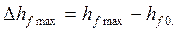 (6.1)
(6.1)
Осыған сәйкес асыра реттеу мынаған тең болады
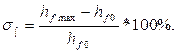 (6.2)
(6.2)
Жүйенiң тербелмелiлiгi реттелетiн шаманың реттеу мерзiмi кезiндегi тербелiс санымен сипатталады. Егер осы уақыт iшiнде жүйедегi өтпелi процесс технология шарты бойынша алдын ала берiлген санынан аз тербелiс жасаса, онда жүйе өзiнiң тербелмелiлiгi жөнiнде қажеттi реттеу талабында деуге болады.
Қалыптасқан статикалық ауытқу 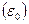 өтпелi процесс аяқталғаннан кейiн реттелетiн шаманың қалыптасқан мәні
өтпелi процесс аяқталғаннан кейiн реттелетiн шаманың қалыптасқан мәні 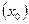 мен оның берiлген мәні
мен оның берiлген мәні 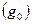 арасындағы айырым түрiнде анықталады:
арасындағы айырым түрiнде анықталады:
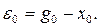 (6.3)
(6.3)
Реттеу жүйесінің сапа көрсеткiштерiн өтпелi процесс графигiнен тiкелей анықтауға болады.
Қажетті реттеу сапасына қол жеткiзу үшiн статикалық дәлдiктi қамтамасыз ету керек. Статикалық қате реттеуiштiң жалпы күшейту коэффициентін арттыру арқылы азайтылуы мүмкiн.
Жалпы күшейту коэффициентiн арттыруда оның шектеулi болуы әрқашан қажет, өйткені күшейту коэффициентін үлкен етiп алған кезде реттелетiн параметрдiң өтпелi процесте тиiмсiз тербелiсi (тiптi орнықсыздығы) пайда болуы ықтимал. Статикалық қатенi азайтуда басқа да нұсқаулар болуы ықтимал, атап айтқанда, әрекетi бойынша статикалық қате болмайтындай етiп реттеуiштiң схемасын өзгерту. Мысалы, статикалық реттеуiштi астатикалықпен алмастыру. Реттеу сапасын жалпы және өтпелi процестiң сапасын iшiнара арттыруды реттеуіштiң құрылымдық схемасына қосымша буындарды ендiру жолымен жүзеге асыруға болады. Қосымша буындардан тұратын, реттеу динамикасын жақсартуға арналған құрылғылар түзетуші құрылғылар деп аталатын құрамды түзедi.
Дәріс 11. Өтпелі процесстердің интегралдық баға сапасы. Баға сапасының жиіліктік әдістері. Орнықталған режимдерде баға дәлдігін реттеу
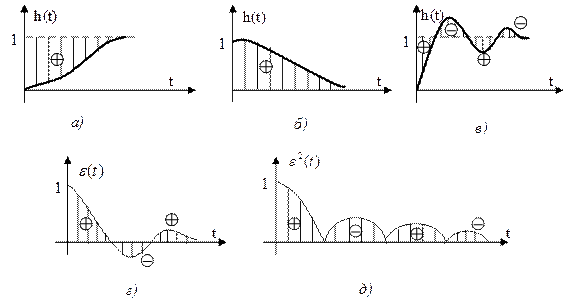
Интегралдық әдіс негізінде өшпелі процесс қисығы мен реттелетін шаманың берілген мәні арасындағы ауданды зерттеу қағидасы жатады (6.3-сурет). Себебі бұл аудан реттеуге кететін шығынды жанама сипаттайды.
Бұл қағида бойынша: реттелетін шаманың берілген мәні мен өтпелі процесс қисығы арасындағы аудан неғұрлым кішкентай болса, соғұрлым реттеу сапасы жоғары. Көбінесе келесі түрдегі интегралдық бағалау кең тараған:
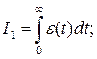 (6.11)
(6.11)
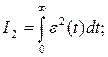 (6.12)
(6.12)
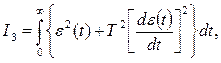 (6.13)
(6.13)
мұндағы 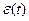 - реттелетін шаманың берілген мәнінен ауытқуы ( реттеу қателігі);
- реттелетін шаманың берілген мәнінен ауытқуы ( реттеу қателігі); 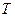 - осы жүйе үшін өтпелі процесті өзгертуге мүмкіндік туғызатын қайсыбір экспоненттің уақыт тұрақтысы.
- осы жүйе үшін өтпелі процесті өзгертуге мүмкіндік туғызатын қайсыбір экспоненттің уақыт тұрақтысы.
Көрсетілген интегралдарды минималдау арқылы реттеу сапасының ең жоғары көрсеткіштерін қамтамасыз ететін параметрлердің мәндерін (АРЖ дифференциалдық теңдеуінің коэффициенттерін) табуға болады.
Интеграл (6.11) реттелетін шаманың берілген мәні мен өтпелі процесс қисығының арасындағы аудандардың алгебралық (яғни, таңбаларын ескере отыра) қосындысын анықтайды. Сол себептен ол тербелмелі емес 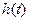 бірсарынды процестерді (6.3,а,б,в,г-сурет) бағалау үшін қолданылады. Тербелмелі өтпелі процестің (6.3,д-сурет) сапасын (6.12) және (6.13) интегралдары бойынша бағалаған дұрыс.
бірсарынды процестерді (6.3,а,б,в,г-сурет) бағалау үшін қолданылады. Тербелмелі өтпелі процестің (6.3,д-сурет) сапасын (6.12) және (6.13) интегралдары бойынша бағалаған дұрыс.
Дата добавления: 2016-10-17; просмотров: 2698;
