Айнымалы электромагниттік өрістің потенциалдары үшін теңдеулер.

Электродинамиканың негізгі теңдеулердін жазамыз:

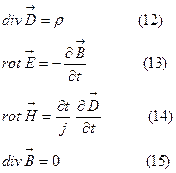
Мұндағы 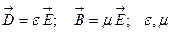-ортаның қасиеттерін сипаттайтын параметрлер (егер орта біттекті болса, онда бұл параметрлер-тұрақты сандар болады). Келесі қосымша функцияларды енгізе отырып (12)-(15) теңдеулер жүйесін біршама ықшамдауға болады: 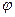-скаляр және 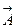векторлық функцияларды енгізерсіз; оларды потенциалдар деп атайды. Бұл функцияларды қалай қорытатынын көрсетеміз.

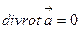тендігін ескере отырып, (15) теңдеудің негізінде 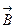векторымен

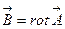(16)

қатынасы арқылы байланысқан жаңа қайсыбір белгісіз 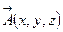функциясын енгізуге болады.

(16)- өрнекті (13) теңдеуге қойып және координаттар мен уақыт бойынша туындылардың коммутитивтігін ескере отырып, мынаны аламыз:

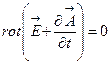
теңдігін ескерсек, мына теңдікті қанағаттандыратын саляр функцияны енгізуге болады.

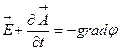
Ендеше

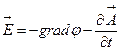(17)

Сонымен біз 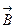және 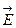-ні жаңа 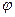және 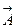функциялары арқылы өрнектеуін.

Бұл функциялар бірмәнді емес анықталғанын тексеруге болады.

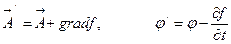мұндағы

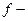дифференциалданатын функция

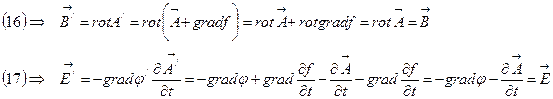
Ендеше, берілген электромагниттік өрісті әр түрлі потенциалдардын жиынымен жазуға болады. Потенциалдардың бір мәнді еместігін пайдаланып потенциалдар үшін жазылған теңдеулерді ықшамдауға мүмкіндік беретін қосымша шарттарды қоюға болады. Оны калибровка шарты деп атайды. Бұл қосымша шртты мына түрде таңдау ыңғайлы

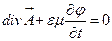(18)

(16),(17) формулаларды Максвелл теңдеуіне қойып және (18) шартты ескере отырып, потенциалдар үшін екі бірдей теңдеу аламыз:

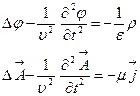
Бұл теңдеулер- Даламбер теңдеулері деп атайды.

Лекция №10.