Нелинейные по параметрам парные уравнения регрессии.

1. Рассмотрим нелинейное уравнение регрессии 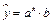. Прологарифмируем обе части равенства 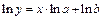. Выполнив замену 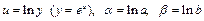, получаем линейное уравнение регрессии 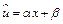. Коэффициент эластичности вычисляется по формуле

.

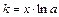2. Прологарифмируем обе части уравнения регрессии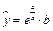

.

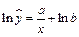Сделаем замену 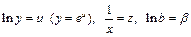. В результате приходим к линейному уравнению регрессии 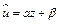. Коэффициент эластичности вычисляется по формуле:

.

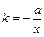3. Аналогично приводится к линейному уравнению регрессии 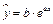, 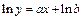. Сделав замену 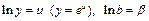, получим 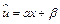. Коэффициент эластичности находится по формуле

.

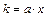4. Рассмотрим уравнение 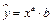. После логарифмирования 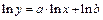и замены 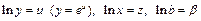приходим к линейному уравнению регрессии 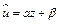. Коэффициент эластичности

.

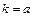5. Рассмотрим показательно-степенную регрессию 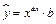. После логарифмирования 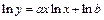и замены 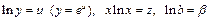приходим к линейному уравнению регрессии 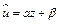. Коэффициент эластичности находится по формуле

.

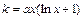6. Рассмотрим нелинейную регрессию 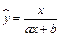. Перепишем уравнение в виде 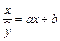. После замены 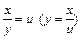, приходим к линейному уравнению регрессии 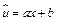. Коэффициент эластичности вычисляется по формуле

.

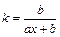Во всех случаях, рассмотренных в п.1.1, 1.2 по крайней мере, в результате одной из замен 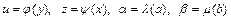нелинейное уравнение регрессии сводится к линейному 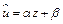. В соответствии с (1.3), (1.5) формулы для оценки параметров принимают вид

.

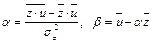После этого из уравнений 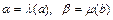находим а и b и записываем уравнение регрессии в исходных переменных х и у.

Для оценки адекватности нелинейной модели парной регрессии также используется критерий Фишера. Наблюдаемое значение критерия находится по формуле

,

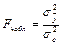где 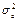– дисперсия ошибок (ср. с SSE, MSE)

,

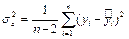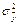– сумма квадратов, которая объясняет регрессию (ср. с SSR, MSR)

.

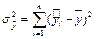По заданному уровню значимости 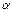и числу степеней свободы 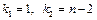по таблице находится критическое значение 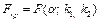. Если 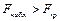, то с надежностью 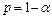можно считать, что рассматриваемая математическая модель адекватна экспериментальным данным. В противном случае рассматриваемую парную регрессию нельзя считать адекватной.

Коэффициент детерминации вычисляется по одной из формул

.

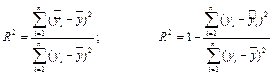После этого можно вычислить индекс корреляции (корреляционное отношение).

Отметим, что наблюдаемое значение 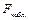критерия Фишера можно выразить и через коэффициент детерминации по формуле

,

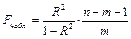где для парного уравнения регрессии .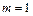

Доверительный интервал для промежуточных значений 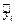и прогноза находится следующим образом:

1) сначала находится доверительный интервал 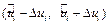для промежуточных значений 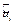и доверительный интервал 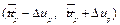для прогноза 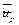линейного уравнения регрессии 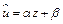, где

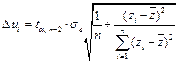
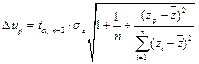
где .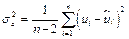

(ср. соответственно с формулами (1.25), (1.24));

2) затем по найденным значениям 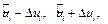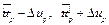, используя связь между переменными и и y из уравнения 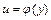, находим соответствующие значения переменной y.