Основные предпосылки в множественном регрессионном анализе.

Основные предпосылки:

1) математическое ожидание случайного отклонения 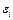равно нулю для всех наблюдений;

2) модель гомоскедастическая, т.е. дисперсии отклонений постоянные и равны для всех наблюдений;

3) случайные отклонения независимы друг от друга;

4) случайное отклонение независимо от объясняющих переменных, т. е ковариация между случайной величиной 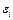и каждой независимой переменной 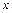равняется 0;

5) модель линейна относительно параметров;

6) случайные отклонения 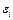распределены нормально с нулевым математическим ожиданием и постоянной дисперсией;

7) отсутствие мультиколлинеарности между факторами , т.е. факторы должны быть независимыми между собой. Другими словами, не должно быть точной линейной зависимости между двумя или большим числом факторов.

Допустим, что есть линейная зависимость между факторам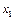и и 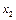. В таком случае не возможно определить отдельное влияние каждого из этих факторов на зависимую переменную . Графически это можно пояснить, исходя из круговых диаграмм.

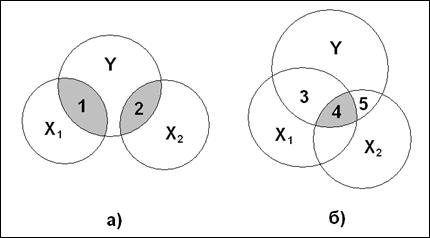
Рис. 3.1. Связь между факторами:

а) отсутствие зависимости между факторам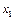и и :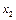

б) наличие такой зависимости.

На рисунке 3.1 изображены два случая. В случае а) отсутствует зависимость или коллинеарность между 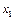и 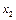; в случае б) – она присутствует. В случае а) подмножество 1 описывает отдельное влияние фактора 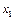на зависимую переменную , а подмножество 2 – отдельное влияние фактора 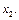При наличии коллинеарности (случай б) подмножество 3 описывает отдельное влияние фактора 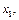а подмножество 5 – отдельное влияние фактора 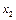. Подмножество 4 характеризует совместное влияние обоих факторов на переменную , которое нельзя отделить. Именно подмножество 4 графически описывает ситуацию коллинеарности.