Вычисление неизвестных коэффициентов множественной регрессии методом наименьших квадратов.
Пусть имеется 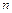 значений случайных величин
значений случайных величин 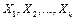 и случайной величины
и случайной величины 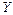 :
:
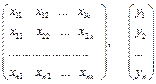 .
.
Рассмотрим оценку линейной корреляционной зависимости
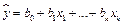 (3.1)
(3.1)
случайной величины 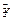 от случайных величин
от случайных величин 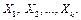
Найдем выборочные средние 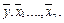 выборочные дисперсии
выборочные дисперсии 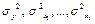 и выборочные средние квадратичные отклонения по формулам:
и выборочные средние квадратичные отклонения по формулам:
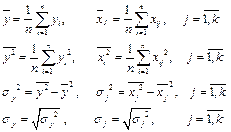 (3.2)
(3.2)
Найдем выборочные коэффициенты корреляции
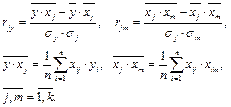 (3.3)
(3.3)
Результаты записываем в виде корреляционной матрицы
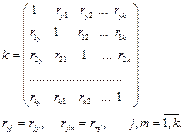
Используя критерий Стьюдента, проверим значимость коэффициентов корреляции. Для этого используется случайная величина
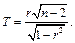
Подставляя в эту формулу вместо 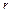 значения
значения 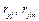 найдем наблюдаемые значения критерия
найдем наблюдаемые значения критерия 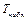 . По таблице критических точек распределения Стьюдента по заданному уровню значимости
. По таблице критических точек распределения Стьюдента по заданному уровню значимости 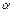 и числу степеней свободы
и числу степеней свободы 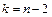 находим критическую точку
находим критическую точку 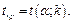 Если
Если 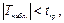 то нет оснований отвергать нулевую гипотезу. Если
то нет оснований отвергать нулевую гипотезу. Если 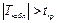 , то нулевую гипотезу отвергают. Если нет основания отвергнуть нулевую гипотезу для коэффициентов
, то нулевую гипотезу отвергают. Если нет основания отвергнуть нулевую гипотезу для коэффициентов 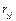 , то это означает, что результативный признак
, то это означает, что результативный признак 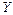 и фактор
и фактор 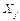 не связаны линейной зависимостью. В этом случае фактор
не связаны линейной зависимостью. В этом случае фактор 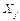 исключается из рассматриваемой модели и дальнейшие вычисления производятся без этого фактора.
исключается из рассматриваемой модели и дальнейшие вычисления производятся без этого фактора.
Исключить несуществующие факторы из рассматриваемой модели можно и иначе, записав уравнение парной линейной регрессии. Используя найденные коэффициенты корреляции, получим уравнения линейной регрессии  на
на 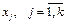
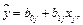
где 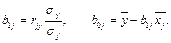
Найдем коэффициенты детерминации (см.(1.16)).
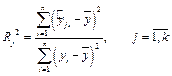
где 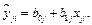
Напомним, что 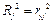 (см.(1.19)). Последняя формула служит для контроля правильности вычисления.
(см.(1.19)). Последняя формула служит для контроля правильности вычисления.
Затем подобно тому, как в п.9, гл.І проверяется адекватность парных уравнений линейной регрессии. Если какое-то уравнение является неадекватным, то между соответствующей независимой переменной 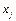 и зависимой переменной
и зависимой переменной  нет линейной связи и эта переменная исключается из рассмотрения.
нет линейной связи и эта переменная исключается из рассмотрения.
В дальнейшем будем считать, что все факторы являются существенными.
Пронормируем случайные величины 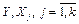
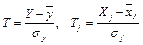 (3.4)
(3.4)
В этом случае, как известно,
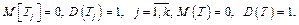
При замене в уравнении (3.1)  на
на 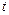 и
и 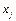 на
на 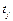 получим
получим
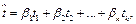 (3.5)
(3.5)
где
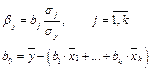 (3.6)
(3.6)
Уравнение регрессии (3.5) называется уравнением в стандартизованном масштабе, а уравнение (3.1) – в натуральном масштабе.
Стандартизованные коэффициенты 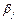 множественной регрессии (3.5) определим на основе метода наименьших квадратов
множественной регрессии (3.5) определим на основе метода наименьших квадратов
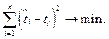
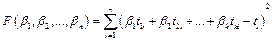
Необходимым условием экстремума функции нескольких переменных является равенство нулю всех частных производных
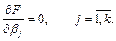
В результате получаем систему
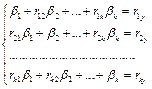 ,
,
где 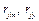 - выборочные коэффициенты корреляции (см.(3.3)).
- выборочные коэффициенты корреляции (см.(3.3)).
Решая эту систему, определим значения коэффициентов 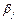 уравнения (3.5) в стандартизованном масштабе.
уравнения (3.5) в стандартизованном масштабе.
Значения коэффициентов 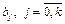 уравнения (3.1) в натуральном масштабе определим по формулам (3.6).
уравнения (3.1) в натуральном масштабе определим по формулам (3.6).
Уравнение (3.5), используя формулы (3.4), можно переписать в виде
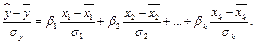
Отсюда следует роль бета-коэффициентов в уравнении. Величина 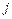 -го стандартизованного коэффициента
-го стандартизованного коэффициента 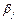 множественной линейной корреляции показывает, что результативный признак
множественной линейной корреляции показывает, что результативный признак 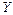 изменится на величину
изменится на величину 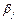 своего среднего квадратичного отклонения
своего среднего квадратичного отклонения 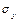 при изменении
при изменении 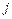 -го фактора на одно среднеквадратичное отклонение
-го фактора на одно среднеквадратичное отклонение 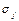 при фиксированных на средних уровнях значениях остальных факторов.
при фиксированных на средних уровнях значениях остальных факторов.
Другими словами, 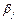 выражает скорость изменения среднего значения функции по каждому из аргументов при постоянных значениях остальных аргументов.
выражает скорость изменения среднего значения функции по каждому из аргументов при постоянных значениях остальных аргументов.
При анализе уравнения регрессии (3.1) вместо коэффициентов 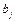 удобнее использовать частные коэффициенты эластичности
удобнее использовать частные коэффициенты эластичности
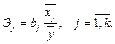
Они показывают на сколько процентов, в среднем, изменяется результативный признак при изменении какого-либо фактора на один процент при фиксированном положении остальных факторных признаков.
Дата добавления: 2016-05-11; просмотров: 1111;
