Множественная линейная регрессия.

Обычно зависимую переменную в регрессионном анализе называют результативным признаком (признаком), а независимую переменную – фактором. Часто наблюдается случай, когда признак зависит не от одного, а от многих факторов. Тогда вместо парной линейной регрессии используют множественную линейную регрессию

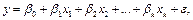
где - зависимая переменная (признак);

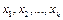– независимые переменные (факторы);

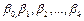– параметры модели, которые необходимо оценить;

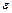– непредсказуемая случайная величина.

Неизвестные параметры обобщенной модели являются постоянными, а случайная величина – непредсказуемой. В отличие от обобщенной регрессионной модели, выборочная модель строится для определенной выборки; неизвестные параметры выборочной модели являются случайными величинами, математические ожидания которых равняются параметрам обобщенной модели.

Выборочная линейная множественная модель имеет вид

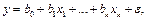
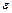- случайная величина (ошибка).

Рассмотрим оценку линейной корреляционной зависимости