Квазилинейное уравнение регрессии.
Наиболее распространенной моделью в экономике является линейная регрессия. Однако не все экономические процессы можно ею моделировать. Поэтому на практике используются и более сложные модели с нелинейной зависимостью между показателем у и фактором х. По методике оценки параметров рассматриваются парные нелинейные регрессии двух видов: 1) нелинейные по факторам, но линейные по неизвестным параметрам, которые подлежат оценке; 2) нелинейные по факторам и параметрам.
Регрессии, нелинейные по факторам, но линейные по оцениваемым параметрам, называются квазилинейными.
Парную квазилинейную регрессию можно записать в общем случае следующим образом
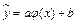 .
.
Заменой переменной 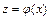 нелинейная парная регрессия сводится к линейной парной регрессии
нелинейная парная регрессия сводится к линейной парной регрессии 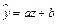 .
.
Коэффициент эластичности в экономике определяется по формуле
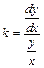 .
.
Он означает на сколько процентов изменится показатель у, если фактор х изменится на 1%. Для квазилинейного уравнения регрессии формула принимает вид
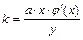 .
.
Рассмотрим ряд частных случаев парной квазилинейной регрессии.
1. Уравнение регрессии 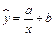 заменой переменной
заменой переменной 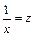 сводится к линейному уравнению регрессии
сводится к линейному уравнению регрессии 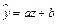 . Коэффициент эластичности вычисляется по формуле
. Коэффициент эластичности вычисляется по формуле
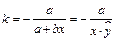 .
.
2. Уравнение регрессии 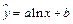 заменой
заменой 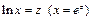 сводится к линейному уравнению регрессии
сводится к линейному уравнению регрессии 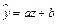 . Коэффициент эластичности вычисляется по формуле
. Коэффициент эластичности вычисляется по формуле
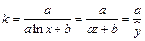 .
.
3. Уравнение регрессии  заменой переменной
заменой переменной 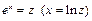 сводится к линейному уравнению регрессии
сводится к линейному уравнению регрессии 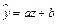 . Коэффициент эластичности вычисляется по формуле
. Коэффициент эластичности вычисляется по формуле
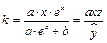 .
.
4. Уравнение регрессии 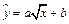 заменой переменной
заменой переменной 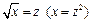 сводится к линейному уравнению регрессии
сводится к линейному уравнению регрессии 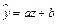 . Коэффициент эластичности вычисляется по формуле
. Коэффициент эластичности вычисляется по формуле
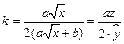
5. Уравнение регрессии 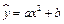 заменой
заменой 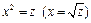 сводится к линейному уравнению регрессии
сводится к линейному уравнению регрессии 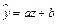 . Коэффициент эластичности вычисляется по формуле
. Коэффициент эластичности вычисляется по формуле
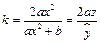 .
.
6. Аналогичным образом уравнение 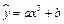 заменой
заменой 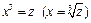 сводится к линейному уравнению регрессии
сводится к линейному уравнению регрессии 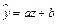 . Коэффициент эластичности вычисляется по формуле
. Коэффициент эластичности вычисляется по формуле
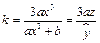 .
.
7. Рассмотрим регрессию нелинейную по показателю 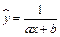 . Перепишем уравнение в виде
. Перепишем уравнение в виде 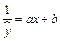 . Заменой
. Заменой  уравнение сводится к линейному
уравнение сводится к линейному 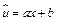 . Коэффициент эластичности вычисляется по формуле
. Коэффициент эластичности вычисляется по формуле
 .
.
8. Более сложной, с точки зрения замены переменных, является уравнение регрессии вида 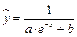 .
.
В этом случае необходимо сделать замену обеих переменных 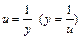 ,
, 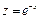 . Тогда нелинейное уравнение регрессии сведется к линейному
. Тогда нелинейное уравнение регрессии сведется к линейному 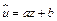 . Коэффициент эластичности находится по формуле
. Коэффициент эластичности находится по формуле
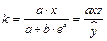 .
.
Дата добавления: 2016-05-11; просмотров: 1681;
