Проверка простой регрессионной модели на адекватность.

Раньше мы показали, что адекватность простой линейной регрессионной модели можно проверить с помощью коэффициента детерминации. Если его значение близко к единице, то можно считать, что модель адекватна. Если его значение близко к нулю, то модель неадекватна, то есть нет линейной связи между независимой и зависимой переменными (заметим это не означает, что случайные величины не коррелируют. Они могут быть связаны другой формой связи корреляционной зависимости). Но какой можно делать вывод, если значение коэффициента детерминации имеет нечетно выраженное граничное значение, например, 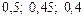и т.д. Понятно, что в таких случаях тяжело сделать однозначный вывод про наличие связи, т.е. про адекватность модели. Нужен другой критерий, который однозначно отвечал бы на вопрос об адекватности построенной модели. Наиболее распространенным является критерий Фишера.

Средние квадраты MSE и MSR (1.20), (1.21) являются функциями от зависимых переменных, поэтому будут случайными величинами, т.е. имеют свое распределение, математическое ожидание, дисперсию и моменты.

В теории вероятностей доказывается, что величина

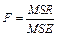(1.22)

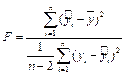(1.23)

имеет распределение Фишера с 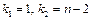степенями свободы. В качестве нулевой гипотезы рассматривается гипотеза 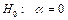о равенстве нулю углового коэффициента линейной модели при конкурирующей гипотезе .

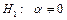Критерий Фишера позволяет проверить нулевую гипотезу 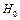о том, что лучше аппроксимировать эмпирические данные средним значением ( 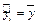), а не регрессионной прямой 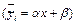. Это дает возможность проверить наличие или отсутствие линейной связи между переменными, другими словами, адекватность построенной регрессионной модели реальной действительности.

На первом этапе по формуле (1.23) по эмпирическим данным вычисляют наблюдаемое значение критерия .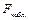

На втором этапе по заданному уровню значимости 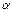и числу степеней свободы 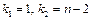по статистическим таблицам 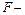распределения Фишера находится критическое значение .

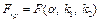Если 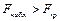, то нулевая гипотеза отвергается, т.е. построенная линейная регрессионная модель адекватна реальной действительности.

Если 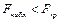, то нет основания отвергнуть нулевую гипотезу.

Пример 3.Вернемся к примеру 1. Проверим полученную ранее модель (1.6) по критерию Фишера.

Таблица 1.3.

i

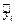
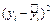
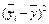
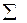
Найдем средний квадрат, который объясняет регрессию, и средний квадрат ошибок:

, ,

, .

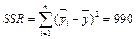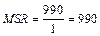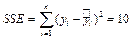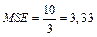Найдем наблюдаемое значение критерия 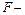распределения Фишера:

.

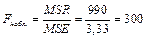По таблице распределения Фишера по уровню значимости 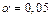и числу степеней свободы 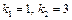находим критическое значение .

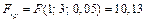Так как 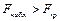, то построенная модель адекватна реальной действительности.