Прогноз в моделях линейной регрессии.
Вернемся к рассматриваемому примеру. Мы имеем ряд значений независимой переменной x (затраты на рекламу) и зависимой переменной у (доход от продажи продукции). На основании этих данных мы построили линейную модель. Поскольку модель адекватна, то можно прогнозировать изменение объема продажи продукции в зависимости от изменения затрат на рекламу. При этом можно получить два типа прогноза: точечный и интервальный. Точечный прогноз дает значение зависимой переменной для соответствующего значения 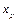 на основании построенной модели
на основании построенной модели
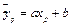 .
.
При этом, исходя из общей модели, действительное значение у для прогноза равняется
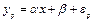 ,
,
где 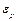 – значение случайной величины.
– значение случайной величины.
Таким образом, значение прогноза  является оценкой истинного значения переменной
является оценкой истинного значения переменной 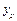 .Полученный прогноз является точечной оценкой. Исходя из полученного точечного прогноза, можно построить доверительный интервал, в который с заданной вероятностью попадает истинное значение зависимой переменной. Такой доверительный интервал при заданном уровне значимости
.Полученный прогноз является точечной оценкой. Исходя из полученного точечного прогноза, можно построить доверительный интервал, в который с заданной вероятностью попадает истинное значение зависимой переменной. Такой доверительный интервал при заданном уровне значимости 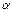 находится по формуле
находится по формуле
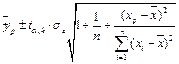 (1.24)
(1.24)
где 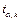 – значения критерия Стьюдента при заданном уровне значимости
– значения критерия Стьюдента при заданном уровне значимости 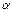 и числе степеней свободы
и числе степеней свободы 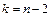 ,
, 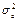 – дисперсия ошибок,
– дисперсия ошибок, 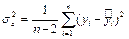 .
.
Обратим внимание, что доверительный интервал становится шире по мере удаления х от своего среднего значения, так как, чем дальше от центра, тем меньше уверенность в значении спрогнозированного значения y.
На практике больше используется построение доверительного интервала для математического ожидания  , т.е. доверительный интервал для
, т.е. доверительный интервал для
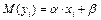 .
.
Формула доверительного интервала для промежуточных значений  имеет вид:
имеет вид:
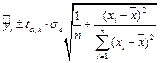 (1.25)
(1.25)
Пример 4.Продолжим рассмотрение зависимости объема реализации продукции от затрат на рекламу. Напомним, что построенная модель имеет вид 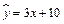 .
.
Найдем значение прогноза объема реализации продукции при затратах на рекламу 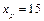 :
: 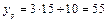 . Построим доверительный интервал зависимой переменной. Дисперсию ошибок
. Построим доверительный интервал зависимой переменной. Дисперсию ошибок 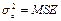 мы находили в предыдущем примере:
мы находили в предыдущем примере: 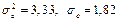 . Заметим, что
. Заметим, что 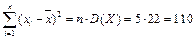 . При уровне значимости
. При уровне значимости 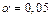 и числу степеней свободы
и числу степеней свободы 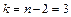 по таблице распределения Стьюдента находим
по таблице распределения Стьюдента находим 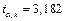 .
.
Таким образом,
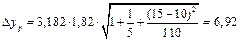 .
.
Доверительный интервал имеет вид 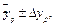 т.е.
т.е. 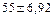 или
или 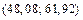 .
.
Дата добавления: 2016-05-11; просмотров: 778;
