Плотность распределения вероятностей.

Нагляднее всего непрерывную случайную величину можно представить тогда, когда ее функция не только непрерывна, но и дифференцируема (за исключением, может быть, конечного числа точек).

Рассмотрим приращение F(x) на интервале (х, х + Dх):

DF(x)= F(х + Dх)– F(x)=P(х £ X 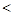х + Dх),

Тогда существует производная

,

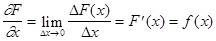которая называется плотностью распределения вероятностей. Кривая, соответствующая уравнению y= f(x), называется кривой вероятностей. График F(x) в точке х имеет касательную, тангенс угла наклона которой равен плотности f(x)вэтой точке.

Описание распределения непрерывной случайной величины с помощью плотности вероятности f(x) более удобно, чем с помощью функции распределения F(x), так как позволяет наглядно передать его особенности на различных участках изменения случайной величины. Однако вероятность попадания случайной величины в заданный интервал предпочтительнее вычислять с использованием F(x).

Свойства плотности вероятностей.

1. Плотность 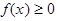, как производная от неубывающей функции F(x).

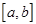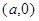2. Вероятность попадания случайной величины в заданный интервал равен площади, ограниченной сверху плотностью распределения вероятностей , снизу осью абсцисс и прямыми, проходящими через точки и 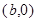, параллельно оси ординат, т.е.

.

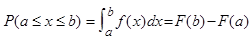Из этой формулы получим следующие формулы:

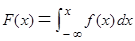и .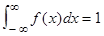

Здесь мы воспользовались свойством функции .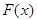

В качестве примера рассмотрим распределение вероятностей в задачах об управлении запасами.

Пусть шеф-повар некоторого ресторана заказывает продукты на воскресенье. Сколько килограммов определенного продукта он сможет использовать? Если бы его ресторан посещало одно и тоже число людей, то никакой проблемы не было бы. Однако в городских условиях число посетителей зависит от многих факторов, в частности от того, какое меню и развлечения предлагают своим гостям другие рестораны. По своему опыту шеф-повар знает, что очень редко количество заказанных продуктов в точности соответствует спросу, а это приводит к материальным потерям. Чтобы тщательно изучить спрос, шеф-повар начал заказывать продукты с некоторым избытком, а затем каждое воскресенье записывал фактический спрос. По полученным данным построил распределение. Пусть оно имеет вид

.

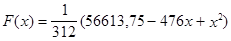Правильно ли будет вычислить теперь среднее значение и закупать на каждое воскресенье именно такое количество продуктов? Будет ли в перспективе это самой разумной политикой? Ответ положительный, но только в том случае, если стоимость излишков, которые будут иметь место в некоторые из воскресных дней, будет равна потерям, связанным с нехваткой продуктов в некоторые воскресные дни.

Пусть 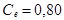долл. – стоимость 1 кг продукта, который оказался в избытке, а долл. представляет собой потерянную в связи с нехваткой 1кг продукта прибыли. Шеф – повара интересует некоторая оптимальная величина x кг, причем 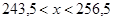. Если спрос окажется меньше x, то убыток будет определяться величиной , если больше x, то величиной 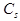. Для фиксированного значения х вероятность того, что D < x, равна F(x). Буквой D обозначается величина спроса.

Определим оптимальное значение х. Оно должно быть таким, чтобы выполнялось равенство

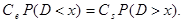
Учитывая, что P(D > x) = 1 – P(D < x), получим

P(D < x)+ 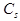P(D < x) = 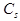или

P(D < x )( + 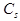) = 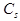, откуда

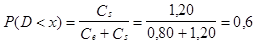или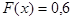

Для нахождения х решим квадратное уравнение

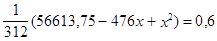относительно х. Получим

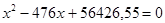и 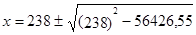, откуда

, .

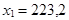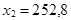Значение 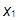не удовлетворяет условию .

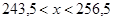Следовательно, шеф-повару следует заказывать 252,8 кг продуктов на каждое воскресенье. Разумеется, для каждого конкретного воскресенья это количество может оказаться или чрезмерным, или недостаточным. Тем не менее, для длительного промежутка времени приведенный метод даст самое лучшее решение.

Аналогичные задачи, когда приходится принимать решение в условиях неопределенности, часто возникают на практике. Так, руководитель фирмы должен все время решать, сколько единиц продукции того или иного вида ему следует произвести, заказать или запасти, чтобы он мог максимизировать прибыль ли минимизировать возможные потери.