Виды случайных величин и их распределения.
Начнем с примера. Будем фиксировать число выпавших гербов при подбрасывании двух монет (Г-герб, Р-решка). В зависимости от исходов (опыта) это число может оказаться равным 0,1 и 2. Построим математическую модель данного опыта. Элементарные события:
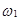 = {Г,Г},
= {Г,Г}, 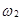 = {Г,Р},
= {Г,Р}, 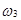 = {Р, Г},
= {Р, Г}, 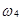 = {Р, Р }.
= {Р, Р }.
Число выпавших гербов является функцией от элементарного события:
Х( 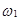 ) = Х{Г,Г} = 2; Х(
) = Х{Г,Г} = 2; Х( 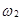 ) = Х{Г,Р} = 1; Х(
) = Х{Г,Р} = 1; Х( 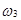 ) = Х{Р, Г} = 1; Х(
) = Х{Р, Г} = 1; Х( 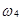 ) = Х{Р,Р}=0.
) = Х{Р,Р}=0.
Исход опыта является случайным событием, поэтому значение Х также является случайным. Функция Х = Х( 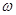 ) – случайная величина, определенная на множестве событий
) – случайная величина, определенная на множестве событий
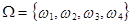 .
.
Если монета симметричная, то элементарные события 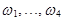 равновозможны и поэтому в математической модели опыта естественно считать вероятности
равновозможны и поэтому в математической модели опыта естественно считать вероятности
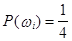 ,
, 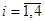 .
.
Зная вероятности P( 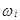 ) можно найти вероятность того, что случайная величина Х примет то или иное значение. Рассмотрим, например, событие
) можно найти вероятность того, что случайная величина Х примет то или иное значение. Рассмотрим, например, событие 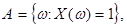 состоящее в том, что Х примет значение 1.
состоящее в том, что Х примет значение 1.
Событие А наступит, если реализуется одно из элементарных событий 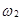 или
или 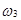 ,
,
т.е. А= { 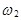 ,
, 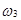 }. Тогда
}. Тогда 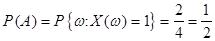 .
.
Случайная величина характеризует количественный результат испытания. Случайной величиной называется функция Х=Х( 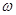 ), определенная на множестве элементарных событий
), определенная на множестве элементарных событий 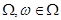 . Случайная величина в результате опыта принимает то или иное (но только одно) значение, причем заранее, до опыта, не известно, какое именно.
. Случайная величина в результате опыта принимает то или иное (но только одно) значение, причем заранее, до опыта, не известно, какое именно.
Случайные величины обозначают прописными латинскими буквами X,Y,Z, ..., а возможные значения случайной величины на элементарном событии – строчными латинскими буквами 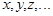
Например, Х – число гербов при подбрасывании двух монет. 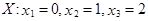 .
.
Y – число солнечных дней в сентябре месяце.
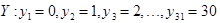 .
.
Z – число детей в семье. 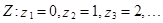
Виды случайных величин.
В практических задачах обычно используются два вида случайных величин – дискретные и непрерывные.
Определение. Случайную величину называют дискретной, если множество ее возможных значений конечно, либо счетно, т.е. их можно перенумеровать натуральными числами.
Примеры приведены выше.
Для описания случайной величины необходимо указать не только множество ее возможных значений, но и вероятности, с которыми принимаются те или иные значения. Такое полное описание случайной величины называется ее законом распределения.
Общими законами распределения для дискретной случайной величины являются: 1) ряд распределения; 2) полигон (многоугольник) распределения; 3) функция распределения.
Рядом распределения дискретной случайной величины Х называется таблица, в которой перечислены возможные значения 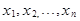 случайной величины X и соответствующие им вероятности
случайной величины X и соответствующие им вероятности 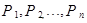 . В любом распределении совокупность событий
. В любом распределении совокупность событий 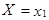 ,
, 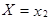 , ... ,
, ... , 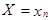 образуют полную систему событий, следовательно,
образуют полную систему событий, следовательно, 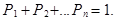
| Х | 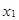
| 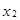
| ... | 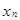
|
Р( 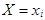 ) )
| 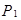
| 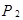
| ... | 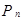
|
Графическое изображение ряда распределения называется многоугольником, или полигоном, распределения. Строится он следующим образом: по оси абсцисс откладываются возможные значения случайной величины Х, а по оси ординат соответствующие им вероятности 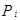 , i=1, 2, ..., n. Соединив соседние точки
, i=1, 2, ..., n. Соединив соседние точки 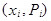 отрезками, получим полигон распределения дискретной случайной величины Х.
отрезками, получим полигон распределения дискретной случайной величины Х.
Пример. В лотерее 100 билетов, среди которых один выигрыш в 40 долл., 5 выигрышей по 20 долл., 10 выигрышей по 10 долл. и 15 – по 5 долл.. Составить ряд распределения случайной величины X – суммы выигрыша на один билет.
Решение.
| |||||
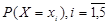
| 0,69 | 0,15 | 0,10 | 0,05 | 0,01 |
|
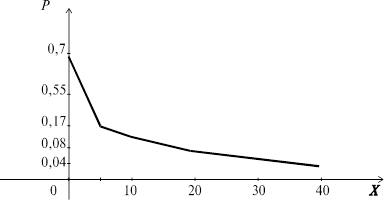
Полигон распределения суммы выигрыша.
Однако не все случайные величины могут быть описаны так просто, как дискретные случайные величины. Например, доход фирмы может, в принципе, принимать любые значения от нуля до бесконечности (это множество не является счетным). Вероятность того, что доход будет в точности равен некоторому значению, будет равна нулю. Ненулевыми будут вероятности только сложных событий: например, доход фирмы будет от 3000 $ до 5000 $. Для подобных (так называемых непрерывных) случайных величин мы не можем задать их распределение путем указания вероятностей каждого возможного значения, так как все эти вероятности равны нулю. При описании таких случайных величин используются другие средства. В частности, если возможные значения случайной величины являются вещественные числа, то распределение случайной величины полностью определяется ее функцией распределения (см. ниже).
Примеры непрерывной случайной величины: рост, вес, возраст случайно встреченного человека, доход на одного человека в месяц, дневная выручка в магазине и др.
Определение. Функцией распределения случайной величины Х называется функция F(x), равная вероятности Р(Х< 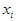 ) того, что случайная величина будетменьше произвольно выбранного значения х.
) того, что случайная величина будетменьше произвольно выбранного значения х.
Ясно, что функция F(x) монотонно возрастает с ростом х (точнее сказать, не убывает, потому что могут существовать участки, на которых она постоянна). У дискретной случайной величины функция распределения ступенчатая, она возрастает скачком в тех точках, вероятности которых не равны нулю. Это точки разрыва F(x).
Функция 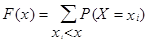 , суммирование ведется по всем значениям i, для которых
, суммирование ведется по всем значениям i, для которых 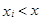 . Следовательно, зная ряд распределения дискретной случайной величины, можно вычислить функцию распределения, представляющую собой функцию накопленных вероятностей.
. Следовательно, зная ряд распределения дискретной случайной величины, можно вычислить функцию распределения, представляющую собой функцию накопленных вероятностей.

|
Пример1. Пусть случайная величина принимает только два значения 0 и 1 с вероятностями р и 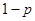 (причем
(причем 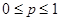 ). В этом случае функция распределения имеет вид:
). В этом случае функция распределения имеет вид:
если х<0
если 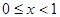 если
если 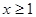
|
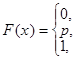
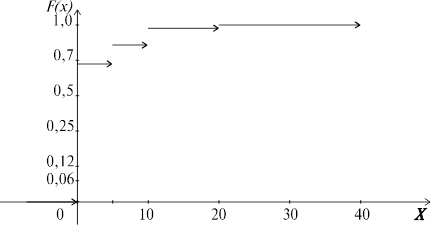
Пример 2. Построить функцию распределения для случайной величины Х – суммы выигрыша на один лотерейный билет (см. пример).
Решение.
| X | |||||
| F(x) | 0,69 | 0,84 | 0,94 | 0,99 | 1,00 |
|
Функция распределения Х – суммы выигрыша на один лотерейный билет.
Для случайной величины, принимающей вещественные значения, то свойство, что вероятность любого отдельного ее значения равна нулю, может легко быть выражено через функцию распределения.
Определение. Случайную величину, принимающую вещественные значения, называют непрерывной, если непрерывна ее функция распределения.
Непрерывным в этом случае называют и соответствующее распределение вероятностей. Для непрерывного распределения вероятность каждого отдельного значения случайной величины равна нулю. На этом и основано противопоставление непрерывных и дискретных распределений – ведь для последних вся единичная вероятность распределена конечными положительными порциями. Для непрерывных же она как бы «разлита» по области определения случайной величины (в данном случае – на прямой). Если в точке х функция распределения y = F(x) имеет скачок,то величина этого скачка равна вероятности, сосредоточенной в точке х, т.е. вероятности события Х = х.
Основные свойства функции распределения.
1. Значения F(x) принадлежат интервалу [0,1], т.е. 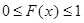 , так как F(x) – вероятность.
, так как F(x) – вероятность.
2. F(x) – неубывающая функция, т.е. 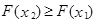 , åñëè
, åñëè 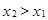 .
.
Вероятность того, что случайная величина Х примет значение из интервала [a,b] равна приращению функции распределения Х на этом интервале (или разности значений F(x) на концах этого интервала), т.е.
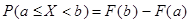 .
.
Вероятность того, что непрерывная случайная величина Х примет одно определенное значение равна нулю. Отсюда следуют равенства:
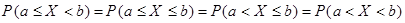 .
.
Поэтому не говорят о вероятности того, что непрерывная случайная величина примет одно значение, а имеет смысл говорить о вероятности попадания случайной величины в интервал, пусть даже и сколь угодно малый.
Примеры.Интересуются вероятностью того, что размеры деталей не выходят за допустимые границы, но не ставят вопрос о вероятности их совпадения с проектным размером.
Вес и рост ребенка не равен заданным нормам, а должен находиться в некотором интервале.
3. Если возможные значения случайной величины принадлежат интервалу [a,b], то F(x) = 0, если õ < a; F(x) = 1, если õ > b.
Пусть 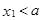 .Тогда событие
.Тогда событие 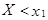 невозможно, так как значений, меньших
невозможно, так как значений, меньших 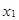 , величина Х по условию не принимает. Вероятность невозможного события равна нулю. Пусть
, величина Х по условию не принимает. Вероятность невозможного события равна нулю. Пусть 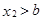 .Тогда событие
.Тогда событие 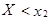 достоверно.
достоверно.
4. 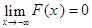 и
и 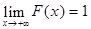 .
.
Условно пишут 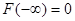 ,
,  .
.
Дата добавления: 2016-06-24; просмотров: 4562;
