Числовые характеристики распределения вероятностей и их свойства
На практике не всегда известен закон распределения вероятностей случайной величины. В этом случае ограничиваются его основными числовыми характеристиками, среди которых различают характеристики: положения (математическое ожидание, мода, медиана и др.), вариации (рассеяния) (дисперсия, среднее квадратическое отклонение , размах и др.) и формы (асимметрия, эксцесс).
3.3.1. Математическое ожидание и его свойства.
Определение. Математическим ожиданием (средним значением по распределению) называется действительное число, определяемое в зависимости от типа случайной величины Х формулой
| ,если Х – дискретная случайная величина |
| , если Х – непрерывная случайная величина |
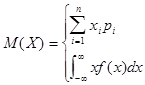
Математическое ожидание (для дискретной случайной величины) существует всегда, если число возможных значений Х конечно. В том случае, если число возможных значений Х счетно, то вместо конечной суммы получим бесконечный ряд и для существования математического ожидания необходимо, чтобы этот ряд сходился абсолютно, т.е.  Для непрерывной случайной величины с плотностью f(x) интервал должен сходиться абсолютно.
Для непрерывной случайной величины с плотностью f(x) интервал должен сходиться абсолютно.
На практике иногда приходится иметь дело со случайными величинами, для которых математическое ожидание не существует.
Пример. Пусть Х принимает значения 1, 2, 3, ... с вероятностями
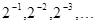 M(X) не существует.
M(X) не существует.
Свойства математического ожидания.
1. Математическое ожидание постоянной равно этой постоянной, т.е.
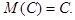
2. Математическое ожидание произведения случайной величины на постоянную величину равно произведению этой постоянной на математическое ожидание случайной величины, т.е.

Доказательство для дискретной случайной величины:
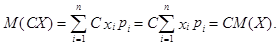
3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий.
Доказательство проведем для суммы двух случайных величин X и Y, учитывая, что X и Y определены на пространстве элементарных событий 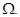

Вероятностный смысл математического ожидания.
Математического ожидание приближенно равно среднему арифметическому, т.е. 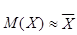 . Причем, чем больше число наблюдений, по которому вычислено среднее арифметическое, тем более точное значение
. Причем, чем больше число наблюдений, по которому вычислено среднее арифметическое, тем более точное значение  будет получено.
будет получено.
Происхождение термина «математическое ожидание» связано с начальным периодом возникновения теории вероятностей (XVI–XVII вв), когда область ее применения ограничивалась азартными играми и страховым делом.
Пример 1. Найти 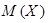 числа появления события А в одном испытании, если вероятность события А равна р.
числа появления события А в одном испытании, если вероятность события А равна р.
Решение. Пусть Х – число появления события А в одном испытании. Тогда 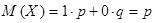 .
.
Пример 2. Найти 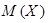 числа появления события А в n независимых испытаниях.
числа появления события А в n независимых испытаниях.
Решение. Пусть Х – число наступления события А в n независимых испытаниях. Оно складывается из числа появлений события в отдельных испытаниях:
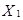 – в первом испытании,
– в первом испытании,
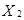 – во втором испытании,
– во втором испытании,
. . .
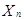 – в n – ом испытании.
– в n – ом испытании.
Тогда X = 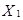 +
+ 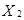 +...+
+...+ 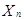 , а
, а

Пример 3. Найти 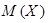 , где Х– число лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, причем вероятность выигрыша на один билет равна 0,3.
, где Х– число лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, причем вероятность выигрыша на один билет равна 0,3.
Решение. 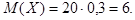
Пример 4. Найти средний выигрыш в лотерее (см. пример §3.1)
Решение. M(X) = 0×0,69 + 5×0,15 + 10×0,1 + 20×0,05 + 40×0,01 = 3,15 долл.
На практике, кроме математического ожидания, которое в определенном смысле характеризует центр распределения вероятностей, применяются и другие характеристики положения, в частности, мода и медиана случайной величины.
Модой непрерывной случайной величины Х называется такое ее значение 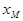 , при котором плотность вероятности имеет максимум. Мода дискретной случайной величины определяется как такое возможное значение
, при котором плотность вероятности имеет максимум. Мода дискретной случайной величины определяется как такое возможное значение 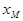 , для которого
, для которого
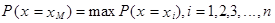 .
.
Таким образом, мода дискретной случайной величины Х есть ее наиболее вероятное значение, если такое значение единственно. Мода может не существовать, иметь единственное значение (унимодальное распределение) или иметь множество значений (мультимодальное распределение).
Медианой 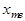 случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины, т.е.
случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины, т.е.
 P(x <
P(x < 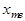 ) = P(x >
) = P(x > 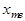 ).
).
Запишем это равенство в помощью распределения
F(x): F( 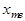 ) = 1 – F(
) = 1 – F( 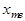 ), откуда F(
), откуда F( 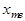 ) =
) = 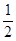 .
.
Дата добавления: 2016-06-24; просмотров: 1121;
