Дисперсия случайной величины и ее свойства.
Многие случайные величины имеют одинаковое математическое ожидание, но различные возможные значения. Поэтому одного математического ожидания недостаточно для характеристики случайной величины.
Пусть доходы Х и Y(в долларах) двух фирм заданы распределениями:
| X | Y | |||||
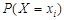
| 0,1 | 0,9 | 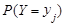
| 0,6 | 0,4 |
Вычислив их ожидаемые доходы, получим M(X) = 980$ и M(X) = 980$, т.е. они равны, хотя возможные доходы и их вероятности различны.
Чтобы оценить, как рассеяны возможные значения случайной величины относительно ее математического ожидания, пользуются числовой характеристикой, которую называют дисперсией.
Определение. Дисперсией случайной величины Х называется неотрицательное число D(X), определяемое формулой
| , если Х – дискретная случайная величина, |
| , если Х – непрерывная случай- ная величина. |
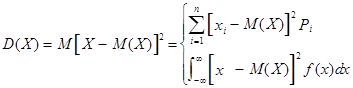
Иногда удобно пользоваться другой формулой, которую можно получить, если воспользоваться свойствами математического ожидания,
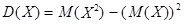 .
.
Дисперсия существует, если ряд (соответственно интеграл) сходится.
Неотрицательное число 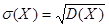 называется средним квадратическим отклонением случайной величины Х. Оно имеет размерность случайной величины Х и определяет некоторый стандартный среднеквадратичный интервал рассеивания, симметричный относительно математического ожидания. Величину
называется средним квадратическим отклонением случайной величины Х. Оно имеет размерность случайной величины Х и определяет некоторый стандартный среднеквадратичный интервал рассеивания, симметричный относительно математического ожидания. Величину 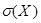 иногда называют стандартным отклонением.
иногда называют стандартным отклонением.
Случайная величина называется центрированной, если 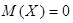 . Случайная величина называется нормированной (стандартной), если
. Случайная величина называется нормированной (стандартной), если 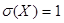 .
.
Продолжим пример. Вычислим дисперсию доходов двух фирм:
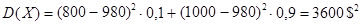
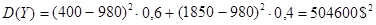
Сравнивания дисперсии, видим, что доход второй фирмы варьирует больше, чем первой.
Свойства дисперсии.
1. Дисперсия постоянной величины равна нулю, т.е. 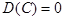 , если
, если 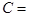 константа. Это очевидно, так как постоянная величина имеет математическое ожидание, равное постоянной величине, т.е.
константа. Это очевидно, так как постоянная величина имеет математическое ожидание, равное постоянной величине, т.е. 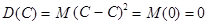 .
.
2. Постоянный множитель C можно вынести за знак дисперсии, предварительно возведя его в квадрат.
Действительно,
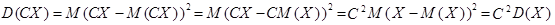
3. Дисперсия алгебраической суммы двух независимых случайных величин равна сумме их дисперсией, т.е.
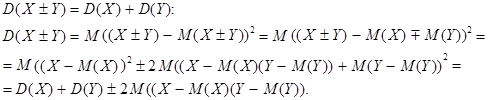
Выражение 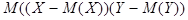 называется ковариацией величин Х и Y (см. Тема 4, §2). Для независимых случайных величин ковариация равна нулю, т.е.
называется ковариацией величин Х и Y (см. Тема 4, §2). Для независимых случайных величин ковариация равна нулю, т.е.
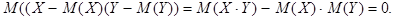
Используя это равенство, можно пополнить список свойств математического ожидания. Если случайные величины Х и Y независимы, то математическое ожидание произведения равно произведению математических ожиданий, а именно:

Если случайная величина преобразована линейно, т.е. 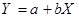 , то
, то
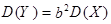 .
.
Пример 1. Пусть производится n независимых испытаний, вероятность появления события А в каждом из которых постоянна и равна p. Чему равна дисперсия числа появлений события А в этих испытаниях?
Решение. Пусть 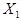 – число появления события А в первом испытании,
– число появления события А в первом испытании, 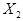 – число появления события А во втором испытании и т.д. Тогда общее число наступления события А в n испытаниях равно
– число появления события А во втором испытании и т.д. Тогда общее число наступления события А в n испытаниях равно
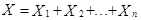 .
.
Воспользовавшись свойством 3 дисперсии, получим
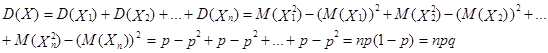
Здесь мы воспользовались тем, что 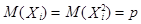 , i =
, i = 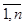 (см. примеры 1 и 2, п.3.3.1.).
(см. примеры 1 и 2, п.3.3.1.).
Пример 2. Пусть Х – сумма вклада (в долларах) в банке – задана распределением вероятностей
| Х | ||||||
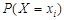 i = i = 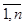
| 0,01 | 0,03 | 0,10 | 0,30 | 0,5 | 0,06 |
Найти среднюю сумму вклада и дисперсию.
Решение. Средняя сумма вклада равна математическому ожиданию
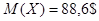 .
.
Для вычисления дисперсии воспользуемся формулой
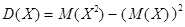 ,
, 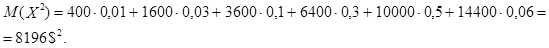
D(X) = 8196 – 7849,96 = 348,04 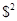 .
.
Среднее квадратическое отклонение 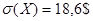
Моменты.
Для того, чтобы учесть влияние на математическое ожидание тех возможных значений случайной величины Х, которые велики, но имеют малую вероятность, целесообразно рассматривать математические ожидания целой положительной степени случайной величины.
Определение. Начальным моментом К-го порядка (K=1, 2, ...) распределения случайной величины Х (если он существует) называется действительное число 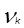 , определяемое формулой
, определяемое формулой
| если Х – дискретная случайная величина, |
| если Х – непрерывная случайная величина. |
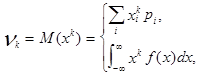
Определение. Центральным моментом К-го порядка распределения случайной величины Х (если он существует) называется число 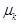 , определяемое по формуле
, определяемое по формуле
| если Х – дискретная случайная величина, |
| если Х – непрерывная случай- ная величина. |
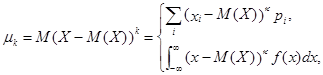
Из определения моментов, в частности, следует, что 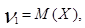
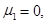
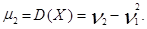
Чтобы приведенные формулы имели смысл, требуется, чтобы суммы и интегралы сходились абсолютно. Так же, как математическое ожидание и дисперсия, моменты существуют не для всех случайных величин.
Дата добавления: 2016-06-24; просмотров: 2359;
