Нормальное распределение.
Нормальное распределение относится к числу наиболее распространенных и важных, оно часто используется для приближенного описания многих случайных явлений, в которых на интересующий нас результат воздействует большое число независимых случайных факторов, среди которых нет сильно выделяющихся. Например, всевозможные измерения (длина, масса, объем, плотность, напряжение и т.д.), с которыми приходится иметь дело в промышленности, имеют распределения, близкие к нормальному. В природе громадное число характеристик также распределено по закону, близкому к нормальному. К ним относятся способности человека, размер и масса живых существ и многое другое.
Однако данные, с которыми приходится иметь дело в экономике, например, ставки заработной платы, цены, товарооборот, уже значительно реже подчиняются нормальному распределению, хотя их логарифмы могут подчиняться нормальному распределению, которое в этом случае называется логарифмически нормальным (логнормальным).
Определение. Случайная величина Х имеет нормальное распределение с параметрами а и 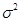 (краткое обозначение
(краткое обозначение 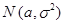 ), если ее плотность распределения задается формулой
), если ее плотность распределения задается формулой
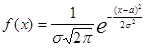 ,
, 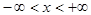 .
.
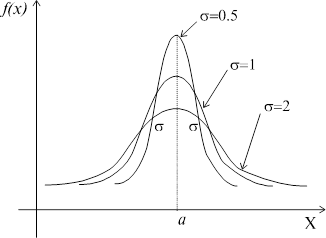
Смысл параметров нормального распределения наглядно показан на рисунке
Отметим, что 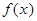 стремится к нулю, если
стремится к нулю, если 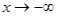 или
или 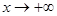 . График функции
. График функции 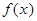 симметричен относительно прямой, проходящей через точку а параллельно оси ординат. В точке х=а
симметричен относительно прямой, проходящей через точку а параллельно оси ординат. В точке х=а 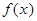 достигает своего максимума, равного
достигает своего максимума, равного 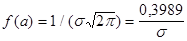 .
.
Параметр а характеризует положение график функции на числовой оси (параметр положения). Если менять его значение, то график функции будет перемещаться параллельно самому себе вдоль оси абсцисс. Параметр 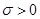 характеризует степень сжатия или растяжения графика плотности (параметр масштаба). Так как площадь, находящаяся под кривой
характеризует степень сжатия или растяжения графика плотности (параметр масштаба). Так как площадь, находящаяся под кривой 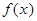 равна 1 (свойство 4 плотности), то при уменьшении
равна 1 (свойство 4 плотности), то при уменьшении 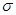 растет
растет 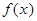 и график ее «стягивается» к своей оси симметрии
и график ее «стягивается» к своей оси симметрии 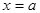 , что соответствует смыслу
, что соответствует смыслу 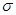 как меры рассеяния.
как меры рассеяния.
Свойства. Математическое ожидание и дисперсия случайной величины 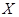 , распределеннойкак
, распределеннойкак 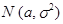 , равны (находятся непосредственным вычислением)
, равны (находятся непосредственным вычислением)
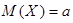 ,
, 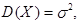
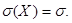
Медиана нормального распределения совпадает с модой и равна a, так как плотность распределения симметрична относительно точки 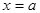 .
.
Особую роль играет нормальное распределение для нормированной случайной величины 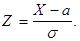 Тогда
Тогда 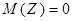 , а
, а 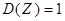 и распределение
и распределение 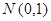 часто называют стандартным нормальным распределением.
часто называют стандартным нормальным распределением.
Плотность нормального стандартного распределения имеет вид
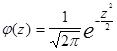 ,
,
а функция распределения стандартного нормального распределения равна
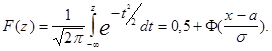
Эта формула позволяет вычислять вероятности событий, связанных с произвольными нормальными случайными величинами, с помощью таблиц стандартного нормального распределения (см. Приложение).
Нормальное распределение впервые было рассмотрено Муавром в 1733г. в качестве непрерывной аппроксимации биноминального распределения. Затем вновь было отрыто и изучено независимо друг от друга Гауссом (1809 г) и Лапласом (1812 г) в связи с работами по теории ошибок.
В практических задачах часто требуется найти вероятность того, что нормально распределенная случайная величина X с параметрами 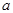 и
и 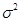 , т.е.
, т.е. 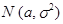 , примет значение из заданного интервала
, примет значение из заданного интервала 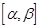 . Воспользуемся формулой
. Воспользуемся формулой 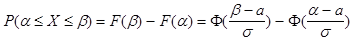 .
.
Пример. Коробки с шоколадом упаковываются автоматически. Их средняя масса равна 1,06 кг. Известно, что 5% коробок имеют массу, меньшую 1 кг. Каков процент коробок, масса которых превышает 940 г? Известно, что вес коробки имеет нормальное распределение.
Решение. По условию задачи 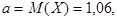
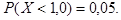
Необходимо определить процент коробок, вес которых удовлетворяет условию
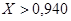 . Воспользуемся формулой
. Воспользуемся формулой
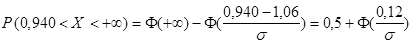 .
.
Неизвестное 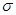 определим из уравнения
определим из уравнения
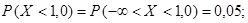
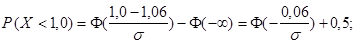
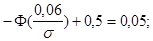
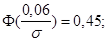
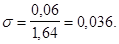
Окончательно
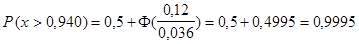 или 99,95%.
или 99,95%.
Найдем формулу для вычисления вероятности отклонения случайной величины X от своегоматематического ожидания а.
Пусть 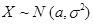 и
и 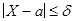 . Тогда
. Тогда 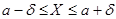 и
и
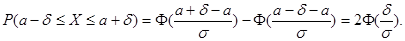
Положим 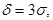 тогда
тогда 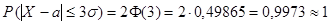 (достоверное событие), а
(достоверное событие), а 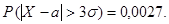
Это равенство может быть сформулировано в виде правила «трех сигма».
Правило: практически достоверно, что отклонение нормально распределенной случайной величины 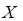 от ее математического ожидания
от ее математического ожидания 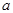 не превысит по абсолютной величине трех сигм.
не превысит по абсолютной величине трех сигм.
Правило «трех сигма» широко применяется в статистике. Так как среди 10000 значений нормально распределенной случайной величины в среднем 27 выйдут за пределы 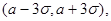 то для небольшого числа значений
то для небольшого числа значений 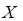 нет таких, которые выходят за пределы указанного интервала. Этим свойством случайной величины часто пользуются при построении вероятностной модели распределения.
нет таких, которые выходят за пределы указанного интервала. Этим свойством случайной величины часто пользуются при построении вероятностной модели распределения.
Иногда интервал 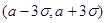 называют интервалом концентрации.
называют интервалом концентрации.
Пример. Случайная величина 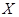 – масса одного зерна распределена нормально с
– масса одного зерна распределена нормально с 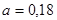 г,
г, 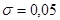 г. Найти:
г. Найти:
а) процент семян, которые дадут хорошие всходы;
б) величину, которую с вероятностью 0,95 не превысит масса одного отобранного зерна.
Хорошие всходы дают зерна, масса которых больше 0,15г.
Решение. а) ( 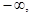 0,15) – плохие всходы,
0,15) – плохие всходы, 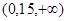 – хорошие всходы,
– хорошие всходы,
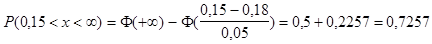 или 72,57%.
или 72,57%.
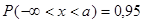 ;
; 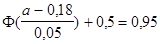 ;
; 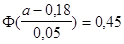 ;
;
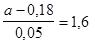 ;
; 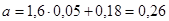 г.
г.
Некоторые приложения нормального распределения.
Пример 1. Заказчику необходимо 5000 стальных булавок. Он определяет нужные ему свойства материала, диаметр булавки и его длину. Длина должна составлять 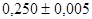 см, т.е.
см, т.е. 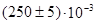 см.
см.
Производитель, чтобы установить, позволяет ли имеющееся у него оборудование удовлетворить требование покупателя, может взять достаточно большую выборку, например, 300 булавок, и вычислить их числовые характеристики. Пусть он получит 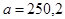 см и
см и 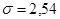 см.
см.
Среднее арифметическое выборки совпадает с требованием заказчика к длине булавки. Как быть с максимально допустимым отклонением 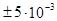 см? В предположении, что значения длины булавок распределены по нормальному закону, в процессе производства будет получен разброс
см? В предположении, что значения длины булавок распределены по нормальному закону, в процессе производства будет получен разброс 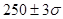 , т.е.
, т.е. 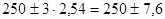 . Разброс слишком велик и некоторое число булавок не будет удовлетворять условиям заказчика. Если внести изменения в процесс производства, то это обойдется в 18$. Поэтому производитель определил число булавок Х, длина которых выходит за заданные пределы (0,245-0,255) см. и сравнил их стоимость (одна булавка стоит 2 цента) с 18$. Это число можно найти, умножив 5000 на вероятность попадания нормально распределенной случайной величины Х в заданный интервал т.е.
. Разброс слишком велик и некоторое число булавок не будет удовлетворять условиям заказчика. Если внести изменения в процесс производства, то это обойдется в 18$. Поэтому производитель определил число булавок Х, длина которых выходит за заданные пределы (0,245-0,255) см. и сравнил их стоимость (одна булавка стоит 2 цента) с 18$. Это число можно найти, умножив 5000 на вероятность попадания нормально распределенной случайной величины Х в заданный интервал т.е.
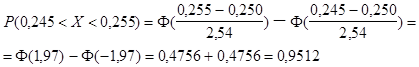
Это значит, что около 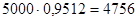 булавок будут удовлетворять стандарту, а
булавок будут удовлетворять стандарту, а 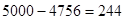 пойдут в брак. Следовательно, убыток составит
пойдут в брак. Следовательно, убыток составит 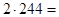 4 доллара 88 центов. Эта сумма существенно меньше 18$. Поэтому производитель может сохранить имеющееся у него оборудование.
4 доллара 88 центов. Эта сумма существенно меньше 18$. Поэтому производитель может сохранить имеющееся у него оборудование.
Пример 2. Пусть владельцу фирмы необходимо заказать 2000 пар женских туфель. Обувь бывает следующих размеров: 35; 35,5; 36; 36,5; ...; 41,5. На основании своего опыта владелец фирмы знает, что размеры обуви распределены по нормальному закону с 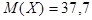 и
и 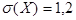 . Сколько пар туфель размера 37 он должен заказать?
. Сколько пар туфель размера 37 он должен заказать?
Прежде чем воспользоваться свойствами нормального распределения, необходимо числу Х = 37 поставить в соответствие некоторый интервал. Пусть это будет интервал 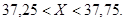 Как и в предыдущем примере, вычислим
Как и в предыдущем примере, вычислим
вероятность
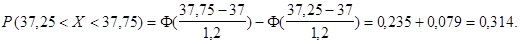
Число пар туфель 37 размера будет равно 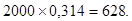
Точно также можно определить и необходимое число туфель всех остальных размеров.
Если владелец фирмы не будет использовать описанную выше методику, то он может понести убытки от того, что туфли некоторых размеров будут лежать непроданными, или не сможет удовлетворить спрос покупателей, что приведет к потере клиентов.
Пример 3. Моделирование с помощью нормально распределенных случайных чисел.
Нормально распределенные случайные числа используются во многих задачах, связанных с моделированием случайных процессов. Рассмотрим пример. В электромоторе имеются детали А и В, причем выход из строя любой из них приводит к остановке двигателя. Началось производство новой модели этого электромотора, и фирма-изготовитель хочет определить распределение ее срока службы. Поскольку двигатель новой модели, то были проведены ускоренные лабораторные испытания, которые позволили установить, что оба распределения можно считать нормальными с числовыми характеристиками 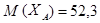 ,
, 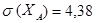 ,
,
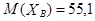 ,
, 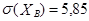 (каждое из чисел умножается на 1000 часов).
(каждое из чисел умножается на 1000 часов).
Электродвигатель собирается на конвейере, где устанавливаются детали А и В. Сколько часов проработает конкретная деталь А ? Возможный вариант ответа 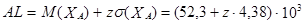 часов. Нам неизвестно, какое значение
часов. Нам неизвестно, какое значение 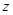 cоответствует той или иной конкретной детали
cоответствует той или иной конкретной детали 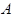 , поэтому берем его из таблицы нормально распределенных случайных чисел и получим оценку срока службы одной детали. Разумеется, для одной детали эта оценка почти заведомо окажется неправильной, но для большого числа таких деталей эти оценки дадут хорошую модель распределения реальных значений срока службыдетали
, поэтому берем его из таблицы нормально распределенных случайных чисел и получим оценку срока службы одной детали. Разумеется, для одной детали эта оценка почти заведомо окажется неправильной, но для большого числа таких деталей эти оценки дадут хорошую модель распределения реальных значений срока службыдетали 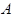 . Аналогично определим срок службы детали B по формуле.
. Аналогично определим срок службы детали B по формуле.
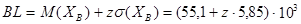 часов.
часов.
Срок службы всего двигателя 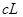 равен
равен 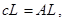 если
если 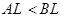 , и
, и 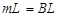 ,
,
если 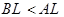 .
.
После того, как некоторое число значений 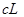 или
или 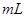 уже получено, можно составить распределение частот. Его можно использовать при организации рекламы новых двигателей и при выработке гарантийных условий его эксплуатации. Проведенный анализ дает фирме возможность организовать рекламу и (или) гарантийное обслуживание. При этом следует иметь в виду, что результаты моделирования можно применять уже в самом начале производства новой модели, поэтому фирме – изготовителю не придется ждать 2-3 года, пока накопятся экспериментальные данные и достаточный опыт эксплуатации.
уже получено, можно составить распределение частот. Его можно использовать при организации рекламы новых двигателей и при выработке гарантийных условий его эксплуатации. Проведенный анализ дает фирме возможность организовать рекламу и (или) гарантийное обслуживание. При этом следует иметь в виду, что результаты моделирования можно применять уже в самом начале производства новой модели, поэтому фирме – изготовителю не придется ждать 2-3 года, пока накопятся экспериментальные данные и достаточный опыт эксплуатации.
Дата добавления: 2016-06-24; просмотров: 3971;
