Гипергеометрическое распределение.
Если производится выборка «без возврата», то вместо биноминального распределения следует применять гипергеометрическое распределение.
Это распределение широко используется в практике статистического приемочного контроля качества промышленной продукции, а также в различных задачах, связанных с организацией выборочных обследований.
Пусть N – число элементов пространства элементарных событий 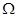 (или генеральной совокупности). Это могут быть изделия, каждое из которых может быть стандартным или дефектным, или семена, каждое из которых может быть всхожим или нет и т.д.
(или генеральной совокупности). Это могут быть изделия, каждое из которых может быть стандартным или дефектным, или семена, каждое из которых может быть всхожим или нет и т.д.
Из соображений экономии нельзя обследовать все пространство 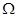 , поэтому используют только часть его (выборку объема
, поэтому используют только часть его (выборку объема 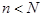 ). Предполагаем, что число N – конечное, а выбранные элементы на место не возвращаются, среди N элементов имеется M, обладающих признаком A, например, дефектные изделия или невсхожие семена. Требуется определить вероятность того, что среди n выбранных элементов будет равно K, обладающих признаком À (см. Рис.).
). Предполагаем, что число N – конечное, а выбранные элементы на место не возвращаются, среди N элементов имеется M, обладающих признаком A, например, дефектные изделия или невсхожие семена. Требуется определить вероятность того, что среди n выбранных элементов будет равно K, обладающих признаком À (см. Рис.).
Определим, как и в схеме Бернулли, вероятность появления события 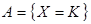 при n испытаниях, используя способ непосредственного подсчета вероятностей. Всего различных способов, которыми можно выбрать n из N равно
при n испытаниях, используя способ непосредственного подсчета вероятностей. Всего различных способов, которыми можно выбрать n из N равно 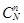 .
.
Среди них благоприятствуют событию A


Следовательно, 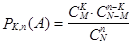 ,
, 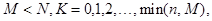 если
если 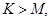 то
то 
n





 M K
M K
N-M n-K
Математическое ожидание гипергеометрического распределения не зависит от N (объема генеральной совокупности) и равно np. В то же время его среднее квадратическое отклонение зависит от N и имеет вид:

 ,
,
т.е. с точностью до конечного множителя 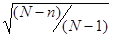 совпадает со средним квадратическим отклонением для биноминального распределения. Если N велико, то эти два распределения совпадают.
совпадает со средним квадратическим отклонением для биноминального распределения. Если N велико, то эти два распределения совпадают.
Пример. Пусть в течение года в 10 номерах еженедельной газеты (всего 52 недели) помещается некоторое объявление. Определить вероятность того, что читатель в 15 произвольно выбранных номерах не встретит это объявление.
Решение. По условию задачи N = 52, M = 10, n = 15. Событие A = {встретить объявление в газете}.
Тогда 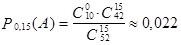 .
.
3.4.4. Геометрическое распределение.
Рассмотрим схему испытаний Бернулли (испытания независимы, вероятность появления события 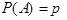 во всех испытаниях одна и та же). Определим вероятность того, что А появится на k-ом испытании, т.е. после того как k-1 раз появилось противоположное событие
во всех испытаниях одна и та же). Определим вероятность того, что А появится на k-ом испытании, т.е. после того как k-1 раз появилось противоположное событие 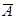 . Обозначим эту вероятность через Г(k,p), тогда Г(k,p)=
. Обозначим эту вероятность через Г(k,p), тогда Г(k,p)= 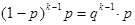 . Меняя значения k от 0 до n, получим геометрическое распределение.
. Меняя значения k от 0 до n, получим геометрическое распределение.
Аналогично можно получить вероятность первого непоявления события А после 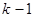 раз его наступления. Она равна
раз его наступления. Она равна 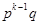 .
.
Пример. Вероятность изготовления нестандартного изделия при некотором технологическом процессе постоянна и равна 0,05. Для проверки качества изготовления изделий контролер берет из партии не более четырех изделий. При обнаружении нестандартного изделия вся партия задерживается. Составить закон распределения числа изделий, проверяемых контролером.
Решение. Пусть случайная величина Х – число нестандартных изделий: 

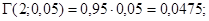
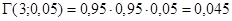 ;
;
P(X = 4)= 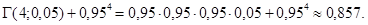
Четвертое изделие проверяется тогда, когда первые три изделия стандартные, а четвертое нестандартное или все четыре изделия стандартные.
| X | ||||
| P | 0,05 | 0,048 | 0,045 | 0,857 |
3.4.5. Равномерное распределение.
Определение. Распределение вероятностей называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения имеет постоянное значение.
Пусть все возможные значения случайной величины Х принадлежат интервалу [a,b]. По определению плотность распределения на этом интервале постоянна и равна некоторой величине 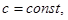 вне этого интервала равна нулю. Определим с из уравнения
вне этого интервала равна нулю. Определим с из уравнения
 (свойство 4 плотности).
(свойство 4 плотности).
 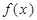
|
 откуда
откуда 
| с |
Имеем 
| 0 a b X |
, если 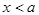 , если
, если 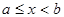 , если
, если 
|

Функцию распределения вычислим по формуле 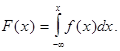 Так как случайная величина
Так как случайная величина 
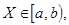 то
то 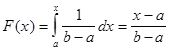 .
.
По определению
, если 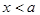 , если
, если 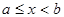 , если
, если 
|

| F(x) |

| 0 a b x |
Математическое ожидание и дисперсию случайной величины Х, распределенной равномерно, вычислим по формулам:
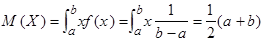 ;
;
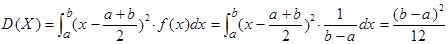 ,
,
 .
.
Область применения. Равномерным распределением описывается время ожидания обслуживания при точно периодическом включении (прибытии) обслуживающего устройства и при равномерно случайном поступлении (прибытии) заявки на обслуживание. Например, время ожидания поезда метрополитена или автобуса пассажиром при условии точных пятиминутных интервалов движения метро или автобуса и случайного момента появления пассажира на остановке будет распределено приближенно равномерно на интервале [0, 5 мин.].
Пример. Светофор на перекрестке работает в двух режимах: 45 сек. горит зеленый свет и 25 сек. – красный и т.д. Водитель подъезжает к перекрестку в случайный момент времени. Найти вероятность того, что он проедет перекресток без остановки.
Решение. Момент проезда автомобиля через перекресток распределен равномерно в интервале, равном периоду смены цветов в светофоре. По условию задачи а = 0, b = 45 сек.+25 сек.=70 сек.=1 мин. 10 сек. Момент проезда перекрестка без остановки должен находиться в интервале (0, 45 сек.). Тогда 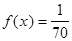 и
и  .
.
Дата добавления: 2016-06-24; просмотров: 997;
