Примеры использования математического ожидания.
Рассмотрим примеры использования математического ожидания на практике для принятия решения в условиях неопределенности.
Пример 1. Анализ имеющихся альтернатив и действий в условиях неопределенности с финансовой точки зрения можно проводить в терминах прибылей и убытков или упущенных возможностей. Рассмотрим задачу, в которой речь идет о возможной прибыли. Представим себе инвестора, владеющего облигациями на сумму 20 000 $. Эти облигации приносят доход 1 200 $/год. В некоторый момент он получил информацию о том, что курс акций на бирже должен повыситься, и ему предстоит принять решение, сохранить ли свои облигации или перевести их в акции.
Будучи знакомым с фирмой, акции которой он думает купить, инвестор считает, что не может получить больше 20% прибыли со своей суммы 20000 $ и не может потерпеть убытки больше чем на 2%. Чтобы проанализировать всю ситуацию более подробно, он перечислил возможные значения Х дохода и приписал каждому значению определенную вероятность, т.е. задал распределение вероятностей дохода с помощью таблицы.
| X$ | ||||||
P(x= 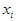 ) )
| 0,0005 | 0,0054 | 0,0269 | 0,0806 | 0,1611 | 0,2256 |
| X$ | -400 | |||||
P(x= 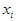 ) )
| 0,2256 | 0,1611 | 0,0806 | 0,0269 | 0,0055 | 0,0004 |
Вычислим ожидаемую прибыль
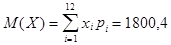 $/год и сравним это значение со своим доходом в 1200 $/год.
$/год и сравним это значение со своим доходом в 1200 $/год.
Означает ли это, что инвестору стоит переключиться с облигаций на акции? Он должен понимать, ожидаемый доход в 1800 $/год есть величина, имеющая смысл для большого числа испытаний. При однократном испытании он может получить любое значение дохода Х, указанное в таблице. Поэтому несмотря на то, что 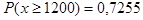 , вполне возможно, что инвестор не будет продавать свои облигации.
, вполне возможно, что инвестор не будет продавать свои облигации.
Пример 2. Пусть лотерейные билеты продаются по 2 $ за штуку, и по ним можно выиграть автомобиль, который стоит 4000 $. Общее число лотерейных билетов равно 8000 и предполагается, что все они будут проданы.
Распределение вероятностей имеет вид  :
: 
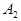
| Возможный исход | Событие 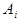
| Вероятность P( 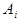 ) )
|
| Выигрыш на один билет | 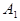
| 1/8000 |
| Проигрыш | 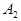
| 7999/8000 |
Таблица 1.
Таблица 2.
|
Вычислим возможный доход (табл.1)( 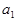 – купить лотерейный билет,
– купить лотерейный билет,  – не покупать билет) и условные потери от неиспользованных возможностей (табл. 2).
– не покупать билет) и условные потери от неиспользованных возможностей (табл. 2).
Ожидаемая прибыль ( 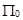 ) равна
) равна
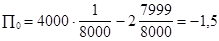 ;
;
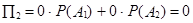 .
.
Ожидаемые потери от не использования благоприятных возможностей равны

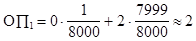 ;
;

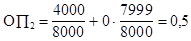 .
.
Отсюда видно, что максимальное значение ожидаемой прибыли равно нулю, а минимальная ожидаемая потеря равна 0,50. Если бы все предполагаемые покупатели лотерейных билетов рассуждали в терминах ожидаемой прибыли и потерь, то лотереи перестали бы существовать. Однако большое число людей не интересуются вероятностью и/или ожидаемой прибылью. Они видят разницу лишь между 4000 $ и 2 $ и понимают, что могут купить лотерейный билет. И все же есть люди, которые рассуждают в терминах вероятностей или возможной прибыли и потерь. В противном случае мы были бы завалены всякого рода лотерейными билетами.
Пример 3. Эта задача касается двух бизнесменов: А и В. В занимается разведкой нефтяных месторождений за границей и просит А предоставить заем в 20 000 $. Он предлагает выплатить этот заем через год плюс 25% этой суммы, т.е. 5000 $.В настоящее время А зарабатывает на этом капитале 1000 $ в год, так что для него это означало бы условную прибыль в 4000 $. Кроме того , В согласен передать А в качестве гарантий займа некоторое имущество, стоимость которого составляет 10 000 $. Бизнесмен А имеет следующие альтернативы:
· «дать заем бизнесмену В и считать, что предприятие последнего окажется успешным» (тогда бизнесмен А заработает 4000 $).
· «одолжить деньги и считать, что В потерпит неудачу и станет банкротом» (в этом случае А потеряет 10 000$).
Определим вероятности событий:
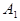 = {успех},
= {успех}, 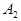 = {неудача}: P(
= {неудача}: P( 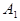 ) = 0,8; P(
) = 0,8; P( 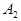 ) = 0,2.
) = 0,2.
Возможные действия: 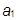 – дать заем,
– дать заем, 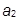 – не давать займа, приведены в
– не давать займа, приведены в
таблице:
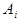
| 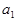
| 
|
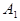
| ||
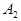
| -10000 |
Числа в каждой клетке соответствуют условным значениям прибыли.
Ожидаемая прибыль: 4000 × 0,8 – 10000 × 0,2 = 1200;
0 × 0,8 + 0 × 0,2 = 0.
Условные потери от использования благоприятной возможность приведены в таблице:
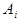
| 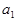
| 
|
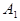
| ||
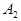
|
Ожидаемые потери от не использования благоприятной возможности:
0 × 0,8 + 10000 × 0,2=2000;
4000 × 0,8 – 0 × 0=3200.
Итак, ожидаемая прибыль составляет 1200 $, и это говорит о том, чтобы серьезно отнестись к предложению В о займе в сумме 20 000 $.
Пример 4. Директор по сбыту издательства, выпускающего воскресную газету, заметил, что значительное число экземпляров газеты иногда оказывается непроданными. Производство каждой лишней газеты обходится в 6 центов. В тех же случаях, когда спрос превышает предложение, издательство теряет возможность заработать 4 цента.
Чтобы получить более точные сведения, директор провел эксперимент: в течение 52 воскресных дней предложение всегда обеспечивало спрос. Данные приведены в таблице:
Число проданных
газет 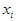 , , 
| Число воскресных дней | |
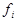
| P( 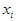 ) )
| |
| 0,12 | ||
| 0,23 | ||
| 0,31 | ||
| 0,21 | ||
| 0,13 | ||
| Всего | 1,00 |
Примечание. 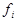 – частота, P(
– частота, P( 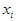 )– вероятность.
)– вероятность.
Следующий этап заключается в составлении таблицы возможных доходов. Обозначим через 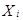 – величину спроса,
– величину спроса, 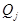 – выпуск того или иного числа газет. Прибыль P = 4 цента за газету. Убыток L = 6 центов за газету. Общий объем прибыли
– выпуск того или иного числа газет. Прибыль P = 4 цента за газету. Убыток L = 6 центов за газету. Общий объем прибыли  при некоторых фиксированных
при некоторых фиксированных 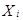 и
и 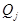 составляет 4Q при
составляет 4Q при 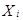 ³
³ 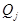 и 4
и 4 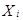 – 6(
– 6( 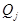 –
– 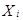 ) = 10
) = 10 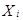 – 6
– 6 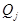 при
при 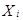 <
< 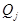 .
.
Например, при i = 2, j = 3 получим доход в сумме 10×24 – 6×25 = 90 (элемент 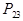 таблицы).
таблицы).
Таблица возможных доходов
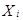
| 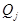
| ||||
Определим ожидаемую прибыль для одного значения 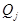 по формуле
по формуле
M( 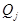 ) =
) = 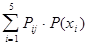 , j = 1,2,3,4,5.
, j = 1,2,3,4,5.
Тогда ожидаемая прибыль для всех 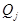 приведена в таблице
приведена в таблице
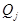
| |||||
M( 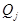 ) )
| 92,0 | 94,8 | 95,3 | 92,7 | 88,0 |
Наибольшее значение ожидаемой прибыли равно 95,3, которое соответствует 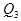 = 25. Это означает , что оптимальный выпуск газет равен 25000. Так как
= 25. Это означает , что оптимальный выпуск газет равен 25000. Так как 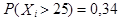 , то следует предполагать, что 34% воскресных дней не будут обеспечены газетами полностью. В некоторых районах такая нехватка может побудить читателей начать покупать другую газету. Это приведет к дополнительным потерям, которые тоже следует оценить, а это не всегда является легкой задачей. В подавляющем большинстве случаев задачу удобно проанализировать в терминах потерь от не использования благоприятных возможностей так, как это было выполнено в примерах 2,3.
, то следует предполагать, что 34% воскресных дней не будут обеспечены газетами полностью. В некоторых районах такая нехватка может побудить читателей начать покупать другую газету. Это приведет к дополнительным потерям, которые тоже следует оценить, а это не всегда является легкой задачей. В подавляющем большинстве случаев задачу удобно проанализировать в терминах потерь от не использования благоприятных возможностей так, как это было выполнено в примерах 2,3.
Дата добавления: 2016-06-24; просмотров: 1788;
