Повторные независимые испытания. Формула Бернулли.

Пусть испытания выполняются по следующей схеме, которая называется схемой Бернулли и удовлетворяет следующим условиям:

1. Испытания независимы, т.е. вероятность события А не зависит от того, появилось или не появилось это событие в других испытаниях.

2. Вероятность появления события А (успех) одна и та же в каждом испытании, т.е. , а .

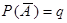3. Испытания могут повторятся n раз при одних и тех же условиях.

Испытаниями Бернулли будут, например, бросание монеты (герб-успех), контроль на стандартность изделия (стандартное изделие-успех), наблюдение за погодой, проводимые в данный день (скажем, 10 февраля) (дождь-успех) и т.д.. Определению испытаний Бернулли не будут удовлетворять бросания по разному искривленных монет (от бросания к бросанию меняется вероятность успеха), наблюдения за погодой в последовательные дни одного года (нет независимости) и т.д..

Рассмотрим следующую задачу.

В условиях схемы Бернулли определить вероятность 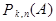события A, состоящего в том, что при n повторных независимых испытаниях событие A произойдет ровно kраз безразлично в какой последовательности.

Пусть , т.е. выполнено одно испытание. Тогда событие A наступит с вероятностью 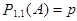или наступит противоположное ему событие 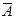с вероятностью .

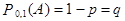Очевидно, что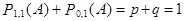

При 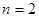произойдет одно из следующих событий: , .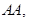

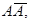
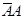Эти четыре события попарно несовместны и одно из них обязательно должно произойти, т.е. они образуют полную систему событий. Вычислим вероятности этих событий. События, входящие в произведения, независимы. Поэтому

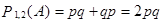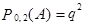, , и

.

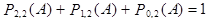Продолжая вычисления для n=3, 4, 5, ..., k, ... убедимся в том, что, если событие А появилось ровно k раз и не появилось n – k раз, то

.

Число таких комбинаций, если взять другую последовательность появления события А, равно . Следовательно,

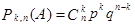, k=0, 1, 2, ..., n.

Эта формула называется формулой Бернулли.

Если вычислить 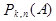для всех значений k и сложить их, то эта сумма будет равна единице, как сумма вероятности событий, образующих полную систему:

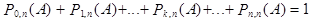
Из этого равенства получим формулу вероятности появления события A хотя бы один раз в n независимых испытаниях

.

Этой формулой можно воспользоваться для вычисления числа опытов n, которые необходимы для того, чтобы с вероятностью 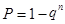можно было утверждать, что событие A произойдет по крайней мере один раз.

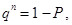
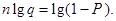Отсюда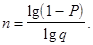

Пример. В лотерее 1000 билетов, среди которых 10 выигрышей по 1млн. рублей, 30 выигрышей по 500 000 рублей, 60 выигрышей по 200 000 рублей и 150 по 60 000 рублей. Найти вероятность кого-нибудь выигрыша при покупке четырех лотерейных билетов.

Решение. Пусть событие A={выигрывает лотерейный билет}; событие {проигрыш}.

Событие А наступит, если произойдет одно из несовместных событий:

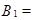{выиграть 1 млн. руб.}, { выиграть 500 000 руб.}, 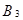={ выиграть 200000 руб.}, 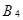={ выиграть 60 000 руб.}, т.е. 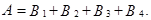По теореме сложения вероятностей найдем:

.

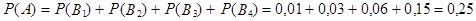Тогда

Отсюда вероятность хотя бы одного выигрыша при покупке четырех лотерейных билетов равна

2.4.2. Наивероятнейшее число появления события при повторении испытаний.

Рассмотрим пример. Садовод сделал осенью 6 прививок. По опыту прошлых лет известно, что после зимовки 7 из каждых 10 черенков оставались жизнеспособными. Какое число прижившихся черенков наиболее вероятно?

Решение. Предположим, что вероятность события A = {привитый черенок приживается} одинакова для всех черенков и равна 0,7 и что испытания независимы. Составим таблицу значения вероятностей для k=0,1,...,6, учитывая, что p = 0,7, q = 0,3, n = 6.

k
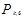
	0,0007	0,0102	0,0593	0,1852	0,3241	0,3025	0,1176

Из таблицы видно, что наибольшая вероятность соответствует событию

B ={приживутся 4 черенка}. Следовательно, это событие более возможно, чем другие.

Решим эту задачу в общем виде.

Обозначим число появлений события A, имеющего наибольшую вероятность, через 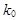. Тогда

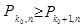и .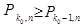

Для первого неравенства имеем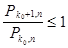

или, учитывая формулу Бернулли,

.

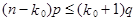После преобразования получим

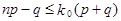или .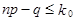

Выполнив те же преобразования для второго неравенства, получим 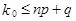. Объединив оба неравенства, получим

.

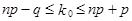Числа и 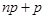отличаются на единицу. Поэтому, если –дробное число, то и 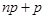также дробное и неравенство определяет одно 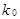. Если –целое, то и 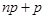–также целое. Тогда 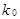и 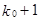будут иметь равную и наибольшую вероятность.

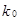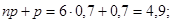
В задаче о садоводе вычислим . Имеем 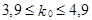. Число 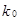-целое, поэтому .

Пример. При установившемся технологическом процессе 80% всей произведенной продукции оказывается продукцией высшего сорта. Найти наивероятнейшее число изделий высшего сорта в партии из 250 изделий.

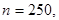
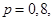
Решение. 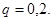Тогда 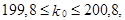следовательно,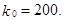

Вычислим вероятность того, что в партии из 250 изделий окажется 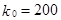изделий высшего сорта, т.е.

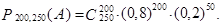
Непосредственное вычисление вероятности является нелегкой задачей. Поэтому английским математиком Муавром (1667–1754 гг.) была предложена в 1733 г. приближенная формула для частного случая, которая затем была обобщена французским математиком, физиком и астроном Лапласом П.С. в 1812 г. и получила гордое название «центральной предельной теоремы» (см. Тема 5, §2).

2.4.3. Локальная и интегральная теоремы Муавра-Лапласа.

Локальная теорема Муавра-Лапласа.

Теорема. Если вероятность наступления события A в каждом из n независимых испытаний постоянна и ровна p 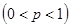, то справедлива при 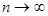следующая приближенная формула

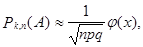
где 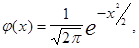а

Формула дает тем более точный результат, чем больше n.

Для функции 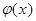составлены таблицы. Так как 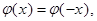то таблицы составлены для значений 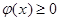(см. Приложение).

Продолжим пример. По условию задачи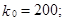

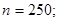
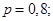
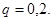
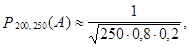так как 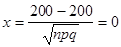и .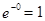

Окончательно, .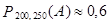

Пример. На опытном поле посеяно 1500 семян. Найти вероятность события A, состоящего в том, что всходы дадут ровно 1200 семян, если считать, что каждое зерно взойдет с вероятностью 0,9.

Решение. Так как n = 1500, k = 1200, p = 0,9, q = 0,1, то

.

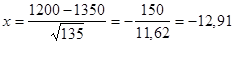По таблице .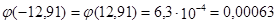

.

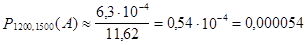Интегральная теорема Муавра-Лапласа.

Теорема. Если вероятность наступления события A в каждом из n независимых испытаний постоянна и равна 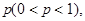то справедлива следующая приближенная формула (при )

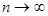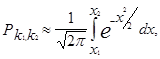
где 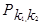– вероятность того, что при n независимых повторных испытаниях событие A наступит не менее чем 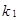раз и не более чем раз,

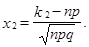
Интеграл не выражается через элементарные функции. Поэтому для вычисления вероятности пользуются таблицей функции Лапласа 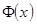(см. Приложение)

.

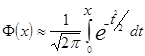Свойства функции .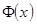

1. Функция нечетная, т.е. 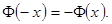Поэтому в таблице приведены значения функции для При x=0,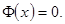

2. Функция 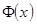, возрастающая на интервале т.к. ее производная положительная при любом x.

3. При .

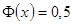Замечание. Имеются таблицы, где .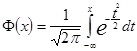

С помощью функции Лапласа вероятность 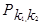можно вычислить по формуле

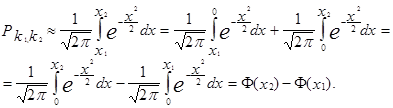
Пример. Вероятность того, что изделие прошло, контроль равна p=0,2. Найти вероятность того, что среди 400 случайно отобранных изделий окажутся прошедшими контроль от 70 до 100 изделий.

Решение. По условию задачи n = 400;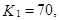

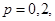
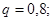
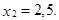
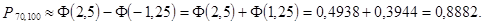
Вопросы для самопроверки.

1. Дайте определение пространства элементарных событий W. Приведите примеры.

2. Какие бывают события?

3. Что называется суммой (объединением) событий; произведением (пересечением) событий? Привести примеры. Дать геометрическую интерпретацию.

4. Дайте классическое и статистическое определение вероятности.

5. Назовите свойства вероятности.

6. Какова связь между вероятностью события и его относительной частотой при большом числе испытаний?

7. Для каких событий A и B справедливо равенство P(A + B) = P(A) + P(B)?

8. Для каких событий A и B справедлива равенство P(A + B) = P(A) + P(B) – P(A×B)?

9. Дайте определение условной вероятности. Для каких событий A и B справедливо равенство P(A×B) = P(A)×P(B)?

10. Привести пример зависимых событий A и B. Найти для этого примера их безусловные и условные вероятности.

11. Написать формулу Байеса и объяснить ее смысл.

12. Написать формулу Бернулли и объяснить смысл входящих в нее букв.

13. Когда используются локальная и интегральная теоремы Муавра – Лапласа?

Задачи.

2.1. Институт имеет 3 филиала в различных городах. Контрольная работа студента поступила из 1-го филиала (событие А), из 2-го филиала (событие В), из 3-го филиала (событие С). Что собой представляют следующие события:

а) А + В; б) 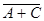; в) АС; г) АВ + С ?

2.2. При выполнении контрольной работы студент получил 3 задания. Введем обозначения: студент выполнил 1-ое задание (событие А), 2-ое задание (событие В), 3-е задание (событие С). Написать выражения для событий, которые состоятся в следующих случаях::

1) студент выполнил только первое задание;

2) студент выполнил только одно задание;

3) студент выполнил только 2 задания;

4) студент выполнил все 3-и задания;

5) студент выполнил хотя бы одно задание;

6) студент выполнил не более двух заданий.

2.3. Предприятие поставляет свою продукцию в 5 магазинов города I, в 2 магазина города У, и в 3 магазина города К. Все магазины пронумерованы от 1 до 10. Со склада отправлена машина в магазин: с четным номером (событие А),с номером, кратным трем (событие В), города I (событие С), города У (событие D), города К (событие Е). Что собой представляют следующие события:

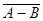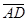1) А + В; 2) С + Е; 3) АD; 4) ; 5) ; 6) – Е ?

2.4. Парламент создает комиссию в составе 4-х человек. Своих кандидатов выдвигают 4 различные партии. От 1-ой партии выдвигают 6 кандидатов, от 2-ой – трех, от 3-й – четырех, от 4-й – пять. Пусть 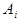( 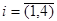)={в состав комиссии выбран депутат i –ой партии}. Составить события:

1) все выбранные депутаты состоят в одной партии;

2) от первой партии выбрано не менее 3-х депутатов;

3) от второй и третьей партии выбрано по 1-ому депутату;

4) все выбранные депутаты состоят в различных партиях.

2.5. Относительно каждой из групп событий ответьте на cледующие вопросы: образуют ли они полную систему событий; являются ли совместными; являются ли несовместными; являются ли равновозможными?

а) Опыт: эксплуатируются две машины в течение времени t;

события: 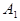={ ни одна машина не вышла из строя}; 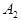={ первая машина вышла из строя, а другая – нет}; ={ первая машина не вышла из строя, а другая – да}; 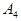={ обе машины вышли из строя}.

б) Опыт: результат работы фирмы;

события: 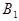= { фирма разорилась}; = { фирма процветает}.

2.6. Комиссия по экологии состоит из 50 человек, из которых 3 представляют данный район Беларуси. Случайным образом выбирается группа из 10 членов комиссии. Что вероятнее: содержит комиссия хотя бы одного представителя данного района или нет?

2.7. Пусть 30% населения некоторого города любит мороженое и не любит пиво, 20% любит пиво и не любит мороженое, а 10% любят то и другое. Чему равна вероятность события C = { население города любит мороженое или пиво}? Житель города, с которым Вы разговариваете, любит мороженое. Чему равна вероятность, что он любит пиво?

2.8. На понедельник запланировано три лекции по различным предметам из 8 изучаемых в данном семестре дисциплин. Какова вероятность того, что студент, не успевший ознакомиться с расписанием, угадает:

1) все запланированные лекции,

2) две из лекций, если любое расписание из трех предметов равновозмоно?

2.9. В мастерскую для ремонта поступило 15 телевизоров. Известно, что шесть из них нуждаются в общей регулировке. Мастер берет первые попавшиеся пять телевизоров. Какова вероятность того, что два из них нуждаются в общей регулировке?

2.10. При приеме партии подвергается проверке половина изделий. Условиями приемки допускается не более 2% бракованных изделий. Определить вероятность того, что партия из 100 изделий, содержащих 5% брака, будет принята.

2.11. Четыре журналиста условились послать свои статьи в четыре различных издательства. Найти вероятность того, что в каждое издательство придет по статье, если журналисты забыли договориться о том, кто в какое издательство посылает статью.

2.12. Восемь человек занимают очередь в кассу за билетами. Среди них находятся 2 друга. Найти вероятность того, что в образовавшейся очереди между друзьями окажется 3 человека.

2.13. На столе находятся экзаменационные билеты, в которых 20 задач по теории вероятностей и 15 задач по статистике. Два студента один за одним выбирают билеты. Найти вероятность того, что:

1) и первый и второй студенты выберут билеты с задачами по теории вероятностей;

2) один по теории вероятностей, другой – по статистике;

3) оба – по статистике.

2.14. При записи фамилий членов некоторого собрания, общее число которых 120, оказалось, что начальной буквой фамилии у двоих была А, у 1-го – Е, у 3 – х –И; у 4-х – О; у 1-го У; а у двух – Ю. У всех прочих фамилии начинались с согласной буквы. Определить вероятность того, что фамилия члена данного общества начинается с гласной.

2.15. Для сообщения об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,95, второй – 0,9. Найти вероятность того, что при аварии поступит сигнал:

а) хотя бы от одного сигнализатора;

б) только от одного сигнализатора.

2.16. В денежно – вещевой лотерее на 1000 билетов приходится 18 денежных и 10 вещевых выигрышей. Некто приобрел два билета. Какова вероятность выигрыша:

1) хотя бы по одному билету;

2) по первому – денег, по второму – вещей?

2.17. Для некоторой местности среднее число дождливых дней в августе равно 14. Чему равна вероятность того, что в первые два дня августа не будет ни одного дождливого дня?

2.18. Студент едет в институт с 2-мя пересадками. Вероятность встречи с контролером в каждом транспорте 0,2. Какова вероятность того, что у студента:

а) ни в одном из транспортов не проверят проездной билет;

б) хотя бы раз проверят билет?

2.19. При выполнении контрольной работы студент решает 4-е задачи. Найти вероятность того, что все задачи будут решены, если вероятность совершить ошибку в 1-ой задаче равна 0,02, во второй – 0,01, в третьей – 0,015, в четвертой – 0,03. События 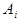={ студент допустил ошибку в i – той задаче } независимы, i= 1,2,3,4.

2.20. В продаже имеются 50 калькуляторов по цене К рублей, 30 – по С рублей и 20 –по L рублей. ( L=2K; C=1,5K ). Какова вероятность того, что стоимость двух купленных калькуляторов не превышает 3K?

2.21. Известно, что 5% всех мужчин и 25% всех женщин дальтоники. На исследование прибыло одинаковое число мужчин и женщин. Наудачу выбранное лицо оказалось дальтоником. Какова вероятность того,что это мужчина?

2.22. Саженец яблони приживается с вероятностью 0,6, груши – 0,5 и винограда – 0,4. Посажено по одному дереву каждого вида. Прижилось два саженца. Какое событие при этом более вероятно: A = {саженец винограда прижился} или B = {саженец винограда не прижился}?

2.23. При переливании крови надо учитывать группу крови больного и донора. Человеку, имеющему 4-ю группу крови, можно переливать кровь любой группы; человеку со 2-ой или 3-ей группой крови можно переливать кровь либо той же группы, либо первой, человеку с 1-ой группой крови – только кровь 1-ой группы. Среди населения 33,7% имеют 1-ую; 37,5% – 2-ю; 20,9%– 3-ю и 7,9% – 4-ю группы крови. Найти вероятность того, что случайно взятому больному можно перелить кровь случайно взятого донора.

2.24. Во время эпидемии гриппа 20% населения города могут подвергнуться воздействию инфекции, из них в определенный промежуток времени могут заболеть 30%, из которых 0,5% могут умереть. Определить вероятность смертности в этот промежуток времени.

2.25. Предположим, что надежность определения туберкулеза при рентгеновском просвечивании грудной клетки составляет 90%, т.е. 10% носителей туберкулеза остаются неопознанными. Вероятность того, что у здорового человека будет ошибочно определен туберкулез, составляет 1%. Просвечиванию подвергнута большая группа людей со средним процентом больных, равным 0,1%. Какова вероятность того, что человек, признанный больным, действительно является носителем туберкулеза?

2.26. Оптовая база обслуживает 8 магазинов. От каждого из них заявка на товар на следующий день может поступить с вероятностью 0,3. Найти наивероятнейшее число заявок на следующий день и вероятность получения базой такого числа заявок.

2.27. Мастерская по гарантийному ремонту телевизоров обслуживает 2000 абонентов. Вероятность того, что купленный телевизор потребует гарантийного ремонта равна 0,15. Какова вероятность того, что число телевизоров, потребовавших гарантийного ремонта, больше 340, но меньше 465?

2.28. На склад магазина поступают изделия, из которых 80% высшего сорта. Найти вероятность того, что из 100 взятых изделий не менее 85 изделий окажутся высшего сорта.

2.29. В автобусном парке ежедневно выходят на линию 100 автобусов. Вероятность выхода из строя двигателя у одного автобуса равна 0,01. Определить вероятность того, что в ближайший день выйдут из строя не более, чем 2 двигателя.

2.30. Среди студентов данного института 60% учатся на хорошо и отлично. Найти вероятность того, что среди 400 случайно опрошенных студентов

1) не менее 260 учатся на хорошо и отлично;

2) не более 200 учатся на хорошо и отлично.

2.31. На склад поступает продукция из 3-х фирм, доля которых составляет соответственно 30%, 32% и 38%. В продукции 1-ой фирмы 60% изделий высшего сорта; 2-ой – 55%; 3-ей – 70%. Найти вероятность того, что среди наугад взятых изделий число изделий высшего сорта заключено между 150 и 200.

2.32. Вероятность того, что при транспортировке компьютеров какой-либо из них выйдет из строя равна 0,002. Найти вероятность того, что не более 2-х компьютеров выйдет из строя при транспортировке 500 компьютеров.