Условная вероятность и теорема умножения вероятностей.
Как отмечалось выше, говорить о вероятности P(A) имеет смысл только при осуществлении определенного случайного эксперимента. При изменении условий эксперимента изменится и вероятность. Так, если к случайному эксперименту, при котором вычислялась вероятность P(A), добавить новое условие, состоящее в появлении события B, то получим другое значение вероятности события A, отличное от P(A).
Событие, состоящее в том, что произойдет событие B, когда известно, что произошло событие À, обозначим символом B/A. Соответствующая вероятность P(B/A) называется условной вероятностью события B при условии, что событие А произошло.
Пример. Колоду из 52 карт можно рассматривать, как пространство элементарных событий 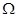 . Предположим, что из множества
. Предположим, что из множества 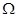 наугад выбрана одна карта и нам сообщили, что она красного цвета. Какова вероятность того, что выбранная карта есть король? Пусть событие K={карта красная}, а R={король}. Сокращенно такую ситуацию можно записать так: P(R/K) – вероятность события R при условии, что событие K произошло. После того, как мы получили информацию о том, что карта красного цвета, мы уже не находимся в исходном пространстве элементарных событий. Нашим новым пространством элементарных событий будет множество, содержащее только 52/2 = 26 карт. Так как среди этих 26 карт имеются ровно два «красных» короля, то P(R/K) = 2/26 = 1/13 » 0,07.
наугад выбрана одна карта и нам сообщили, что она красного цвета. Какова вероятность того, что выбранная карта есть король? Пусть событие K={карта красная}, а R={король}. Сокращенно такую ситуацию можно записать так: P(R/K) – вероятность события R при условии, что событие K произошло. После того, как мы получили информацию о том, что карта красного цвета, мы уже не находимся в исходном пространстве элементарных событий. Нашим новым пространством элементарных событий будет множество, содержащее только 52/2 = 26 карт. Так как среди этих 26 карт имеются ровно два «красных» короля, то P(R/K) = 2/26 = 1/13 » 0,07.
В этом рассуждении нам пришлось перейти к новому пространству элементарных событий.
Получим формулу для вычисления условной вероятности. Пусть пространство элементарных событий 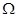 распадается на n равновозможных исходов,
распадается на n равновозможных исходов,
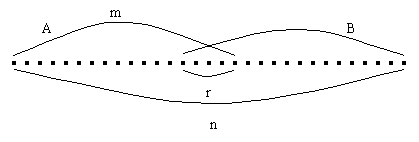
из которых событию А благоприятствуют m исходов, а событию A×B – r исходов. Тогда, если произошло событие А, то число всех равновозможных исходов сократилось до m, а число благоприятствующих исходов для наступления события В равно числу благоприятствующих для A×B. Поэтому
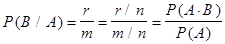 , если
, если 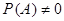 .
.
Аналогично , 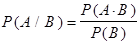 , если
, если 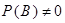 .
.
Из этих формул получим формулу умножения вероятностей:
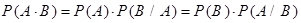 .
.
Это так называемая теорема умножения вероятностей: вероятность совместного наступления двух событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое произошло.
Событие А называется независимым от B, если его условная вероятность равна безусловной, т.е. P(A/B) = P(A). Тогда P(A×B) = P(A)×P(B).
Пример 1. А ={число очков делится на 3} при выпадении игральной кости, т.е. A = { 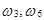 }. B = {выпало четное число очков} = {
}. B = {выпало четное число очков} = { 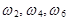 }.
}.
Тогда A×B = { 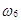 }. По формуле условий вероятности
}. По формуле условий вероятности
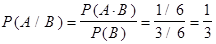 .
.
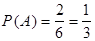 , следовательно события A и B независимы.
, следовательно события A и B независимы.
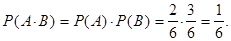
Пример 2. Рассмотрим задачу из анализа решений (см. схему). Предположим, что фирма А собирается объявить конкурс на заключение выгодного контракта. Фирма B располагает достаточной информацией о фирме А для того, чтобы оценить минимально, максимально возможный и промежуточный объем контракта. Обозначим их цифрами I, II и III соответственно. По оценкам фирмы B, вероятность того, что А предложит минимально возможный контракт, равна P(I) = 0,2; а две другие вероятности равны P(II) = 0,5 и P(III) = 0,3. Со своей стороны фирма B может в данный момент участвовать только в одном конкурсе, поэтому она может в каждом из трех случаев легко оценить вероятность того, что ей удастся получить заказ. А именно по ее оценкам P(B/I) = 0,4; P(B/II) = 0,7; P(B/III) = 0,1. Располагая всеми этими данными, фирма B может теперь вычислить вероятность событий типа «А объявляет конкурс на контракт типа I и наша фирма его получает», т.е. вероятности P(I,B), P(II,B) и P(III,B). Вычислим их:
P(I,B) = P(I)×P(B/I) = 0,2×0,4 = 0,08;
P(II,B) = 0,5×0,7 = 0,35;
P(III,B) = 0,3×0,1 = 0,03.

Сумма всех вероятностей должна быть равна единице.
Действительно, 0,08+0,12+0,35+0,15+0,03+0,27=1
Прагматическое правило. Всякое утверждение будет верным лишь с некоторой вероятностью, а с некоторой вероятностью оно может оказаться неверным. Можно высказать следующее прагматическое правило, которым руководствуются люди и которое соединяет теорию вероятностей с нашей деятельностью:
· Мы считаем практически достоверным событие, вероятность которого близка к единице.
· Мы считаем практически невозможным событие, вероятность которого близка к нулю.
Правило полезно тем, что дает возможность практически применять вероятностные выводы.
Иногда то же правило высказывают чуть по-другому: в однократном испытании маловероятное событие не происходит и наоборот обязательно происходит событие, вероятность которого близка к единице.
Какую вероятность следует считать малой? Нет количественного ответа, пригодного во всех случаях. Это зависит от конкретной задачи. Так, надежность технических устройств, например, тормозов автомобиля, требует большей вероятности, чем вероятность попасть под дождь, не взяв зонтика.
2.3.4. Формула полной вероятности.
Эта формула объединяет сложение и умножение вероятностей.
Рассмотрим пример. На двух предприятиях изготавливаются лампочки накаливания, соответственно 70% и 30% общей продукции. Испытания показали, что из 100 ламп первого предприятия 83 выдерживают установленный срок службы, а для второго предприятия – только 63. В среднем из 100 ламп 77 соответствуют указанному условию (83×0,70 + 63×0,3), т.е. вероятность купить такую лампу равна 0,77.
Предположим, что приобретена лампа первого предприятия. Тогда вероятность того, что она исправна, равна 0,83. Безусловная вероятность приобретения исправной лампы равна 0,77; условная вероятность (условие – изготовлена на первом предприятии) равна 0,83.
Ряд очень полезных формул можно вывести, разбивая некоторое исходное пространство элементарных событий на несколько частей и подразделяя затем каждую из этих частей еще на несколько подмножеств. Термин «разбиение» означает, что любая пара этих событий имеет нулевое пересечение.
Так, в рассмотренной ранее задаче, разбиваем все пространство произведенной продукции (100%) на две части ( 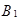 ) 70% и (
) 70% и (  ) 30%. Затем каждую часть делим на две
) 30%. Затем каждую часть делим на две 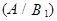 и
и 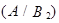 части:
части: 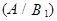 – годная продукция, произведенная на предприятии
– годная продукция, произведенная на предприятии 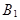 .
. 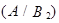 – годная продукция, произведенная на предприятии
– годная продукция, произведенная на предприятии 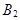 . Тогда, вероятность купить годную лампу равна
. Тогда, вероятность купить годную лампу равна


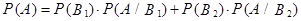 = 0,7×0,83 + 0,3×0,63 = 0,77.
= 0,7×0,83 + 0,3×0,63 = 0,77.
70% 30%
0,37
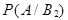 =0,63 =0,63
|
0,17
 =0,83 =0,83
|
 |
Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из событий 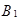 ,
,  , ...,
, ..., 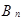 , образующих полную систему, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А,
, образующих полную систему, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А,
 .
.
Доказательство.
Записанную формулу мы можем легко получить, вспомнив, что события 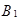 ,
,  , ...,
, ..., 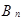 образуют полную систему, т.е. они единственно возможны и попарно несовместны. Событие А может появиться только с одним из несовместных событий
образуют полную систему, т.е. они единственно возможны и попарно несовместны. Событие А может появиться только с одним из несовместных событий 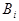 , i=1, 2, ..., n, т.е.
, i=1, 2, ..., n, т.е.
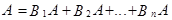 .
.
События  несовместны, что следует из несовместности событий
несовместны, что следует из несовместности событий 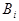 , i=1, 2, ..., n.
, i=1, 2, ..., n.
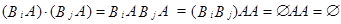 .
.
Вычислим вероятность события А
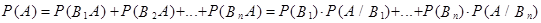 .
.
Пример. Две машины на некоторой фирме производят соответственно 10% и 90% общей продукции некоторого вида. Предположим, что вероятность брака на 1-ой машине равна 0,001 , а на 2-ой 0,05. Чему равна вероятность события А = {изделие бракованное}?
Введем обозначения:
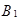 = {изделие произвела 1-ая машина}, 0,9 0,1
= {изделие произвела 1-ая машина}, 0,9 0,1
 = {изделие произвела 2-ая машина}.
= {изделие произвела 2-ая машина}.
Событие А = 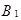 A +
A +  A подразделяется на два несовместных события
A подразделяется на два несовместных события 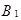 A ,
A ,  A. Поэтому
A. Поэтому
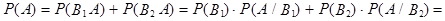
= 0,1×0,01 + 0,9×0,05 = 0,046.
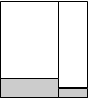
Заштрихованная область – это и есть вероятность P(A) = 0,046
2.3.5 Формула Байeса (английский математик 1702–1762 г.г.)
Пусть в результате испытаний произошло событие А. Оно могло произойти только совместно с одним из событий 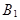 ,
, 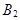 , ...,
, ..., 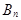 , которые образуют полную систему и безусловные вероятности этих событий известны. Требуется найти вероятности событий
, которые образуют полную систему и безусловные вероятности этих событий известны. Требуется найти вероятности событий 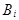 при условии, что событие А произошло. По формуле условной вероятности
при условии, что событие А произошло. По формуле условной вероятности
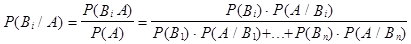 , i=1, 2, ..., n.
, i=1, 2, ..., n.
Мы получили формулу Байеса, которая дает выражение послеопытных вероятностей (апостериорных) через доопытные (априорные) вероятности. 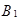 ,
,  , ...,
, ..., 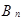 называют гипотезами, поэтому формулу Байеса иногда называют формулой гипотез. Если доопытные вероятности событий
называют гипотезами, поэтому формулу Байеса иногда называют формулой гипотез. Если доопытные вероятности событий 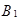 ,
,  , ...,
, ..., 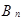 неизвестны, то их полагают равными: P(
неизвестны, то их полагают равными: P( 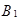 )= P(
)= P(  )= ... =P(
)= ... =P( 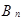 ). Тогда формула упрощается и
). Тогда формула упрощается и
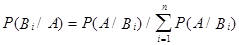 .
.
Формула Байеса может служить основанием для принятия решений после проведения эксперимента. Но для того, чтобы выбор правдоподобной гипотезы имел достаточно оснований, необходимо, чтобы в результате эксперимента ее апостериорная вероятность была достаточно близка к единице.
Пример 1.(продолжение предыдущего). Определить, чему равна вероятность того, что взятое наугад изделие изготовлено первой машиной, если оно оказалось бракованным?
Решение. Необходимо вычислить P( 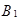 / A) = 0,1×0,01 / 0,046 = 0,022.
/ A) = 0,1×0,01 / 0,046 = 0,022.
Пример 2. На складе имеются приборы, изготовленные тремя заводами. 20% изготовлено 1-ым заводом, 50% 2-ым и 30% 3-м заводом. Вероятности, что в течение гарантийного срока прибору потребуется ремонт, для продукции каждого из заводов соответственно равны: 0,2; 0,1; 0,3 . Взятый со склада прибор не имеет заводской маркировки и потребовал ремонта в течение гарантийного срока. Каким заводом вероятнее всего был изготовлен этот прибор? Какова его вероятность?
Решение. Обозначим через 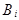 ={прибор изготовлен i-ым заводом}, i=1,2,3, а через А = {прибор дефектный}. Тогда P(
={прибор изготовлен i-ым заводом}, i=1,2,3, а через А = {прибор дефектный}. Тогда P( 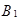 ) = 0,2; P(
) = 0,2; P(  ) = 0,5; P(
) = 0,5; P( 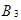 ) = 0,3; P(A/
) = 0,3; P(A/ 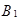 ) = 0,2; P(A/
) = 0,2; P(A/  ) = 0,1; P(A/
) = 0,1; P(A/ 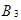 ) = 0,3; P(A) = 0,2×0,2 + 0,5×0,1+0,3×0,3=0,18; P(
) = 0,3; P(A) = 0,2×0,2 + 0,5×0,1+0,3×0,3=0,18; P( 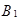 / A) = 0,222; P(
/ A) = 0,222; P(  / A) = 0,278; P(
/ A) = 0,278; P( 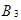 / A) = 0,5. Следовательно, вероятнее всего дефектный прибор изготовлен 3-им заводом.
/ A) = 0,5. Следовательно, вероятнее всего дефектный прибор изготовлен 3-им заводом.
Дата добавления: 2016-06-24; просмотров: 1913;
