Определение вероятности события.

Обратимся теперь к введению понятия вероятности (от латинского слова Probability = P). Так как в основе определения любого события лежит пространство элементарных событий 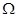, которое будем предполагать дискретным, то понятие вероятности следует, прежде всего, определить для элементарных событий (аксиомы теории вероятностей).

Определение 1. Каждому элементарному событию 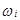соответствует неотрицательное число 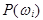, называемое вероятностью элементарного события.

Определение 2. Вероятностью любого события 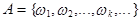называется число 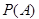, равное сумме вероятностей элементарных событий, входящих в это событие, т.е.

.

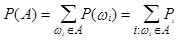Причем

.

Отсюда следует, что всегда 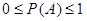, причем вероятность достоверного события равна единице, а вероятность невозможного события равна нулю.

Дискретное пространство элементарных событий с определенным в нем соответствием типа 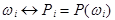называется дискретным вероятностным пространством.

Указанное соотношение может быть задано различными способами: с помощью таблиц, графиков, аналитических формул или алгоритмически.

Из определений 1,2 можно получить ряд свойств вероятности:

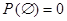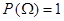1). ; 2). ; 3). ;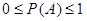

4). Если , то P(A+B)= P(A)+ P(B).

Это свойство известно под названием теоремы сложения для несовместных событий.

Классическое определение вероятности.

Для решения конкретной задачи необходимо находить вероятности P( 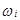) численно.

Здесь возможны два пути – не требующего проведения опытов и прямого измерения. Исторически основой понятия вероятности послужило известное соотношение

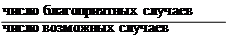
– определение вероятности, данные Я.Бернулли (1654–1705 г.) и П.С.Лапласом (1749–1827г.)

Классическое определение используется тогда, когда пространство всех возможных элементарных исходов состоит из конечного числа n элементов, которые полагаются равновероятными. Так как все P( 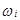) равны между собой и число их равно n

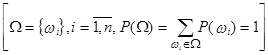, то .

Именно в такой ситуации мы находимся при подбрасывании симметричной монеты, бросании правильной игральной кости, извлечении карты из хорошо перемешанной колоды и т.д. Основная область приложения этого подхода – азартные игры и случайный выбор, т.е. имеет ограниченное применение.

Пусть теперь событию А благоприятствуют m исходов. Тогда .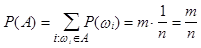

Смысл этой формулы таков: вероятность события А равна отношению числа m благоприятных исходов (т.е. элементарных исходов, входящих в это событие) к числу n всех возможных исходов, если все элементарные исходы равновероятны.

Речь идет при этом об априорной вероятности, которая не требует проведения эксперимента.

Пример 1. Один раз бросили монету. Найти вероятность события A={выпал герб};

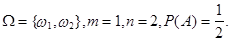
Пример 2. Один раз брошена игральная кость. Найти вероятность события:

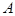={выпала цифра 5}, 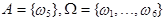; m=1, n=6; .

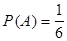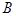={выпало четное число очков}; 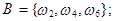m=3, n=6;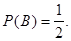

Пример 3. Студент подготовил 20 билетов из 25. Преподаватель задал
3 вопроса. Найти вероятность, что студент знает ответ.

Решение.

, ;

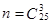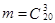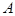={студент знает ответ}; .

Хотя измерение вероятности события отличается от измерения других физических величин, все же прямое измерение ее возможно, оно основано на независимых повторениях случайного эксперимента.

Статистическое определение вероятности.

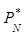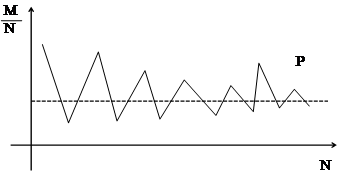
Допустим, что случайный эксперимент, в результате которого может произойти рассматриваемое событие А, многократно повторяется в одинаковых условиях. Если при повторении опыта N раз событие А наступает М раз, то величину (A) называют относительной частотой или частостью наступления события А в данной серии из N испытаний. Оказывается, что при неограниченном увеличении N величина 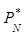(A) колеблется около вероятности события А и неограниченно приближается, к этой вероятности при увеличении числа испытаний (см график). Поэтому на частость можно смотреть, как на результат измерения вероятности и считать P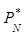(A) » (A) . Однако, как велико может быть различие между 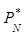(A) и P(A)при данном конечном N, мы пока не знаем: это будет выяснено с помощью центральной предельной теоремы (см. Тема 5,§2).

Указанная связь между частотой события и его вероятностью составляет содержание теоремы Бернулли (см. Закон больших чисел, тема 5,§1).

Вероятность, определяемая статистически, обладает теми же свойствами, что и вероятность.

Для проверки статистического определения вероятности в разное время были произведены различные опыты:

1. Французский естествоиспытатель Бюффон бросал монету 4040 раз, герб выпал 2048 раз, т.е. 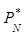(A)=0,5069.

2. Английский статистик Пирсон: а) бросал монету 12000 раз, герб выпал 6019 раз, т.е. 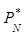(A)=0,5016; б) бросал монету 24000 раза, герб выпал 12012 раз, т.е. 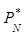(A)=0,5005. Отсюда видно, что с увеличением N, частости меньше отличаются друг от друга и приближаются к числу 0,5 – вероятности события

А = {выпадет герб}.

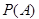
Итак, задав вопрос об измерении вероятностей, мы столкнулись с трудностями, которые возникают на практике: во-первых, оно оказалось непростым с физической точки зрения (многократные повторения опыта в одних и тех же условиях); во-вторых, сопряжено с определением точности приближения частности к вероятности, а также в необходимом числе опытов для достижения заранее указанной точности. Эти вопросы будут рассмотрены ниже. Аксиоматическое определение вероятности принадлежит А.Н. Колмогорову (1933г.), который понятие вероятности построил на основе современной теории множеств, теории меры и на функциональном анализе и тем самым создал теоретический аналог эмпирической относительной частоты.