Общие правила комбинаторики.
Пусть имеется n множеств 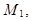
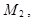 ...,
..., 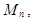 содержащих по
содержащих по 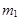 ,
, 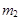 , ...,
, ..., 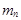 элементов каждое. Выбирается по одному элементу из каждого множества и составляется еще одно множество. Число способов, которыми можно выбрать по одному элементу из каждого множества, равно произведению
элементов каждое. Выбирается по одному элементу из каждого множества и составляется еще одно множество. Число способов, которыми можно выбрать по одному элементу из каждого множества, равно произведению 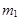
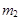 ...
... 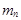 .
.
В этом и состоит основной принцип комбинаторики.
В задачах теории вероятностей часто встречаются различные соединения (комбинации) из множества n элементов по k элементов (k £ n).
Ниже будем рассматривать соединения без повторений, т.е. каждый элемент данного множества может входить в соединения не более одного раза.
Рассмотрим три вида соединений: 1) размещения, 2) перестановки,
3) сочетания.
Определение. Размещениями из n элементов по k элементов называются под- множества k элементов, отличающихся одно от другого или са- мими элементами или их порядком. Число размещений обозна-
чается 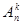 и равно
и равно
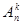 = n (n-1) ... (n– (k-1)) .
= n (n-1) ... (n– (k-1)) .
Доказательство. Для того, чтобы расположить k элементов в определенном порядке, выберем один из них и будем считать его «первым». Это можно сделать n способами. Оставшееся множество содержит n-1 элементов. Из него выберем один и назовем его «вторым». Для выбора второго элемента имеются n-1 способов. Осталось множество из n-2 элементов. Продолжив процесс отбора, последний k-ый элемент можно выбрать n– (k-1) способами. Согласно основному правилу комбинаторики число всех способов, которыми можно составить размещения, т.е. число размещений равно
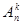 = n (n-1) ... (n– (k-1))=
= n (n-1) ... (n– (k-1))= 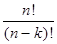 ,
,
где n ! – произведение n первых целых чисел (читается эн-факториал).
Пример. Определить, сколько трехзначных чисел можно составить из множества цифр 1,2,3,4,5 без повторения.
Решение. Имеем n=5, k=3, 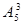 = 5×4×3 = 60.
= 5×4×3 = 60.
Определение. Перестановками из данных n элементов называются множества из n элементов, различающиеся только порядком.
Перестановки – это частный случай размещений, k = n. Поэтому
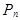 = n (n-1) ... (n– (k-1)) ... 1 =
= n (n-1) ... (n– (k-1)) ... 1 = 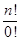 = n !
= n !
По определению принимается 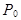 = 0! = 1.
= 0! = 1.
Пример 1. К кассе за получением (или уплатой) денег подошли одновременно 5 человек. Сколькими способами они могут выстроиться в очередь?
Решение. Очередь состоит из пяти различных лиц, поэтому в каждом способе составления очереди учитывается порядок их расположения. Таким образом, имеют место перестановки из пяти человек, их число равно
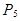 =1·2·3·4·5=120.
=1·2·3·4·5=120.
Определение. Сочетаниями, содержащими k элементов, выбранных из n элементов заданного множества, называются всевозможные множества, различающиеся хотя бы одним элементом. Число сочетаний из n элементов по k обозначают 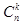 или
или 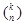 .
.
Число сочетаний из n элементов по k вычисляется по формуле
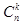 =
= 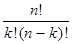 .
.
Доказательство. Рассмотрим размещения из n элементов по k. Их число 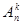 . Если не считаться с порядком элементов в перестановке из k элементов, то существует k! перестановок, которые нельзя отличить от первоначальной перестановки. Поэтому число всех сочетаний
. Если не считаться с порядком элементов в перестановке из k элементов, то существует k! перестановок, которые нельзя отличить от первоначальной перестановки. Поэтому число всех сочетаний 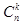 в k!раз меньше числа всех размещений, т.е.
в k!раз меньше числа всех размещений, т.е. 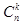 =
= 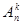 /
/ 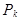 =
= 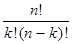 .
.
Пример. Сколькими способами можно выбрать двух студентов в студенческий совет из 20 студентов?
Решение . Имеем n=20, k=2. Способы отбора считаются различными, если каждая отобранная пара различается хотя бы одним студентом, а это
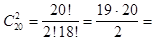 190.
190.
Вопросы для самопроверки.
1. Что является предметом изучения теории вероятностей?
2. Какое явление называется случайным?
3. Какие модели используются для описания социальных и экономических явлений?
4. Приведите формулу вычисления числа размещений из n элементов по k.
5. Приведите формулу для вычисления числа перестановок из n элементов.
6. Приведите формулу для вычисления числа сочетаний из n элементов по k.
Задачи.
1.1. Басня Крылова: «проказница мартышка, осел, козел да косолапый мишка надумали сыграть квартет ...». Сколькими способами они садились?
1.2. Встретились пять человек и обменялись рукопожатиями, а после беседы визитными карточками. Сколько было рукопожатий и визитных карточек?
1.3. К кассе одновременно подошли за получением (или уплатой) денег шесть человек. Сколькими способами они могут выстроиться в очередь?
1.4. Из 20 студентов отбираются 8 человек для стажировки в США. Определить число групп, если шансы быть включенными в группу у всех студентов одинаковы. Сколькими способами можно выбрать из этих восьми человек руководителя группы и его заместителя?
1.5. В соревновании участвуют десять команд. Сколько существует различных возможностей среди этих команд занять призовое (I, II, III) место?
Дата добавления: 2016-06-24; просмотров: 706;
