Случайные события и их классификация.

Теория вероятностей занимается оцениванием правдоподобия, вероятности или шансов на то, что то или иное событие из некоторого множества возможных событий действительно произойдет.

Что мы понимаем под словом «событие»? Каждому вопросу или решаемой проблеме соответствует некоторое множество возможных ответов. В теории вероятностей событием называется произвольное подмножество этого множества.

С каждым случайным экспериментом связано понятие совокупности всех его возможных исходов. Каждый из этих возможных исходов будем называть элементарным (неразложимым) событием (или элементарным исходом), а совокупность всех таких возможных исходов – пространством элементарных событий (исходов).

Таким образом, в результате анализируемого случайного эксперимента обязательно происходит одно из элементарных событий, причем одновременно с ним не может произойти ни одно из остальных элементарных событий (о таких событиях говорят, что они несовместны).

Рассмотрим лишь дискретный случай, т.е. когда все элементарные события можно занумеровать числами 1, 2, 3,...,... Обозначим пространство элементарных событий через 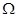, а сам факт «пространство 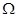состоит из элементарных событий 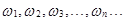кратно обозначим

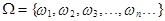или

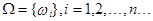
Примеры случайных экспериментов и соответствующих им пространств элементарных событий.

П.1. Подбрасывание монеты – испытание:

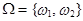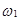, – цифра, 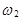– герб.

П.2. Выбрасывание одной игральной кости – испытание:

.

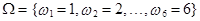П.3. Четырехкратное бросание игральной кости:

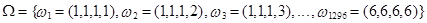, 6⁴ = 1296.

П.4. Проверка (по альтернативному признаку: годная, брак) одного изделия, случайно отобранного из продукции массового производства:

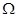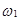={ = годное, 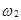=брак}.

П.5. Проверка (по альтернативному признаку) N изделий, случайно отобранных из продукции массового производства:

.

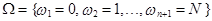П.6. Проверка (по альтернативному признаку) двух выборок, состоящих соответственно из 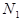и и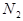зделий, случайно отобранных из продукции массового производства:

.

П.7. Определение 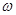– числа сбоев станков автоматической линии за случайно выбранную смену:

.

П.8. Имеются 3 карточки, на каждой из которых написаны буквы к, т, о. Сколько можно составить слов?

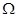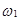={ = (кто), 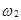=(отк), ..., 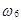=(кот) }.

В самом общем случае задачи теории вероятностей можно разбить на три категории:

1) Найти вероятность того, что реализуется хотя бы один из возможных исходов.

2) Найти вероятность того, что будут иметь место лишь некоторые из возможных исходов.

3) Найти вероятность того, что произойдет событие, не принадлежащее к множеству возможных исходов.

Задача 1. В вероятностных рассуждениях рассматривается множество возможных исходов. Поэтому ясно, что вероятность того, что будет иметь место хотя бы один из них, в действительности превращается в достоверность: некоторое событие обязательно произойдет. Следовательно, пространство всех элементарных событий 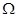является достоверным событием. В примере с игральной костью 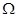– это событие, заключающееся в появлении любого числа от 1 до 6.

Задача 2. Случайным событием А называется любое подмножество пространства элементарных событий W. Поэтому неопределенность наступает тогда, когда мы пытаемся оценить вероятность некоторого конкретного исхода, принадлежащего множеству всех возможных исходов. Естественно, она должна быть меньше вероятности достоверного события.

Задача 3. Событие, не принадлежащее к множеству возможных исходов, называется невозможным (пустым) и обозначается 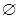(или V). Оно не содержит ни одного элементарного события 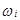. Например, появление числа 0 или 7 при бросании игральной кости.

Событием, противоположным к событию А, называется такое событие 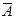, которое состоит из всех элементарных событий, не входящих в А. Иначе, событие 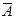состоит в не наступлении события А. Например, событием, противоположным событию А из примера 5, будет событие 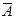, состоящее в том, что число обнаруженных дефективных изделий в партии изделий объема N окажется меньше четырех, если событие А – это число годных изделий, т.е.

, .

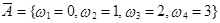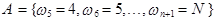Несовместными называются события 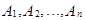, если в результате случайного эксперимента никакие два из них не могут произойти одновременно. Это означает, что среди событий 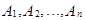нельзя найти такую пару событи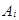й и 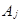, в которой обнаружилось хотя бы по одному общему элементарному событию. Любые пары (А, 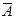) противоположных событий являются несовместными. Такими же являются и элементарные события.