Действия с событиями.

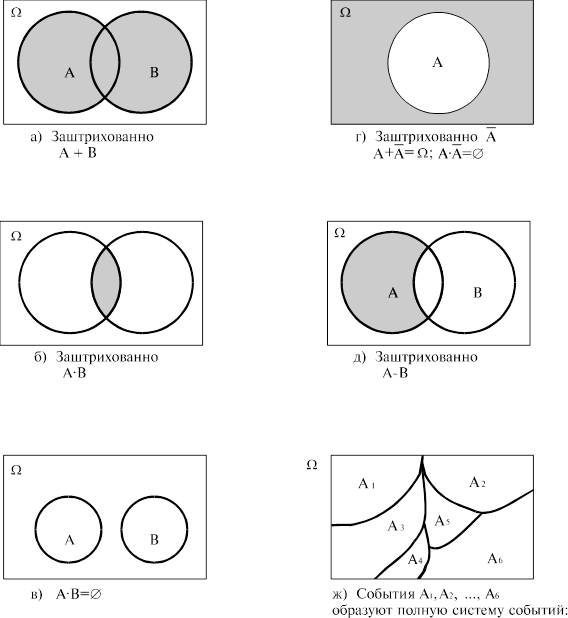
Сумма (объединение)событий 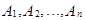– это такое событие 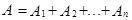, которое заключается в наступлении хотя бы одного из событий 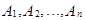. На языке элементарных событий, следовательно, сумма событий 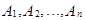определяется как событие А, состоящее из всех различных элементарных событий, составляющих события .

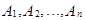Пример. Если 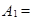{число дефектных изделий не более 4} = = 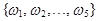, 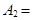{число дефектных изделий заключено между 2 и 6 включительно} = , то .

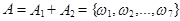Произведение (пересечение) событий 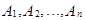– это такое событие или 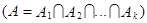, которое заключается в наступлении обязательно всех событий 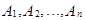и определяется как событие А, состоящее лишь из тех элементарных событий, которые одновременно входят во все рассматриваемые события.

Пример, рассмотренный ранее, .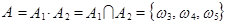

Разность событий и 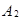– это такое событие А, которое заключается в одновременном существовании двух фактов: событие произошло, а событие 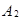не произошло. На языке элементарных событий, следовательно, разность 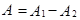определяется как событие, состоящее из всех тех элементарных событий, которые входят в , но не входят в 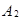. Пример, рассмотренный ранее .

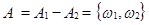Полная система событий – это такой набор несовместных событий 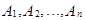, который в сумме исчерпывает все пространство элементарных событий, т.е.

,

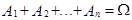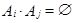для всех i,j=1,2, ..., n и .

Набор всех элементарных событий можно рассматривать как частный случай полной системы событий.

Пример. Пусть N=100, d – число дефектных изделий, обнаруженных в партии, состоящей из N наугад извлеченных изделий:

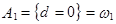– отличное качество;

– брак в пределах допустимой нормы;

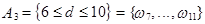– брак выше допустимой нормы;

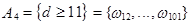– партия возвращается;

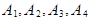образуют полную систему.

Графическое изображение действий с событиями представлено на рис.1

,

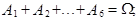
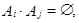
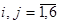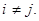
Рис. 1. Круги Эйлера, или диаграммы Венна.