NV - эффективная плотность состояний в валентной зоне (на 1 см3 вещества).
Величина Nа представляет собой концентрацию акцепторов. Так же как и для n – полупроводника, для полупроводников типа p справедливо равенство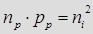 
.
Это равенство означает, что произведение концентраций электронов и дырок при данной температуре T для данного полупроводника постоянно и не зависит от характера и количества примесей.
В силу симметрии выражений, определяющих концентрацию основных и неосновных носителей заряда в примесных полупроводниках, независимо от типа проводимости, их можно записать в следующем виде:
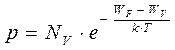- для дырок, 
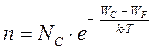-для электронов,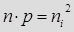 
где WF – уровень Ферми, определяемый для соответствующего типа полупроводника.
Поделив эти выражения друг на друга, приняв при этом n = ni2 / p и p = ni2 / n, можно привести
их к следующему виду: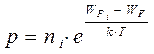 
, 
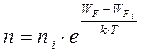
где WFi = (Wc - Wv) / 2 – уровень Ферми в собственном полупроводнике, а WF – уровень Ферми в соттветствующем примесном полупроводнике.
Учитывая, что энергия электрона (дырки) W = q·φ, последние выражения для дырок и электронов соответственно можно привести к виду:
, 
.
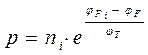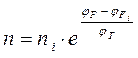где: φF i – потенциал Ферми в (вольтах) собственного полупроводника, φF - потенциал Ферми в (вольтах) соответствующего собственного полупроводника,
φT = k·T/q – температурный потенциал (в вольтах). При комнатной температуре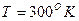 
.
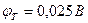В некоторых учебниках, потенциал Ферми в собственном полупроводнике - φFi , заменяют потенциалом середины запрещённой зоны примесного полупроводника - φE, что практически одно и то же, т.к. φFi ≈ φE.
Тогда: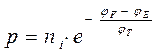 
, 
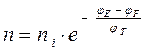
Из этих выражений непосредственно следует:
φFn = φE + φT · ln(n / n i ) – для полупроводников n – типа уровень Ферми смещён от середины запрещённой зоны вверх по диаграмме к свободной зоне на величину ln(n / n i ) и
φFp = φE - φT · ln(p / n i ) – для полупроводников p – типа уровень Ферми смещён от середины запрещённой зоны вниз по диаграмме к валентной зоне на величину ln(p / n i ) .
2.7. Электропроводность примесных полупроводников.
Так же как и для собственного полупроводника, проводимость примесного полупроводника, независимо от его типа : σ = q·n·μn + q·p·μp .
Принимая во внимание, что в электронном полупроводнике n>>p, σn ≈ q·n·μn , а в дырочном полупроводнике p>>n, σp ≈ q·n·μp, проводимость примесных полупроводников в основном определяется концентрацией основных носителей заряда.
Пренебрегая в данном случае концентрацией неосновных носителей, будем остерегаться заблуждения относительно их роли в физических процессах, имеющих место в полупроводниковых приборах.
2.7.1. Зависимость электропроводности примесных полупроводников от температуры.
Зависимость проводимости σ от температуры определяется двумя факторами:
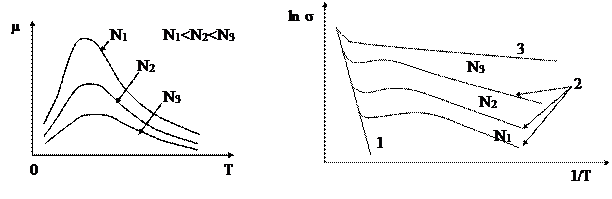- зависимостью концентрации носителей заряда от температуры, а также зависимостью подвижности носителей заряда μn и μp от температуры. В области низких температур подвижность зарядов пропорциональна μ → T 3/2 , а при высоких температурах μ→(1/T)3/2.
2.8. Электрический ток в примесном полупроводнике
Перемещение носителей заряда – электронов и дырок в полупроводнике вызывается двумя причинами.
1) Направленное перемещение под действием электрического поля, называемое дрейфом носителей заряда. Ток обусловленный дрейфом носителей заряда называется дрейфовым.
jn др = q·n·μn·E – для электронного тока, jp др = q·p·μp·E – для дырочного тока.
2) Направленное перемещение носителей заряда вследствие разности концентраций зарядов
(дырок или электронов) в смежных областях полупроводника. Ток, обусловленный
избыточностью заряда в некоторой ограниченной области полупроводника, называется диффузионным, а перемещение носителей заряда, стремящихся равномерно распределитьсяв объёме полупроводника, - диффузией.
jn диф. = q·Dn·grad n - для электронов, jp диф. = -q·Dp·grad p - для дырок.
Здесь Dn и Dp - коэффициенты диффузии электронов и дырок соответственно. Dn,p = φT·μn,p.
Полная плотность электронного и дырочного тока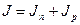 
определяется суммой двух составляющих: 
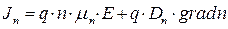- полный электронный ток
и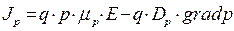 
- полный дырочный ток
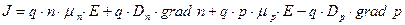
Как правило, нас интересует движение носителей заряда в направлении одной из осей координат.
Обозначив это направление через x, для одномерной модели получим:
jn = jn др + jn диф = q·n·μn·E + q·Dn· д n/dx -для электронов, jp = jp др + jp диф = q·p·μp·E - q·Dp·д p/dx -для дырок.
Как электроны, так и дырки всегда движутся в направлении убывания концентрации носителей заряда, поэтому если выбранное положительное направление оси х совпадает с градиентом, то электронный ток будет иметь положительное направление, а дырочный ток отрицательное. Этим обясняется знак минус перед диффузионной составляющей дырочного тока в приведённых выше выражениях для плотностей токов.
3. КОНТАКТ ДВУХ ПОЛУПРОВОДНИКОВ РАЗЛИЧНОГО ТИПА ПРОВОДИМОСТИ.
3.1.Электронно – дырочный переход.
Под идеальным контактом двух полупроводников понимается такое их соединение, при котором:
1) - граница их раздела является абсолютно плоской.
2) - граница раздела не содержит вкраплений других элементов и дефектов кристаллической решётки, т.е. кристаллическая решётка одного полупроводника непрерывно переходит в кристаллическую решётку другого.
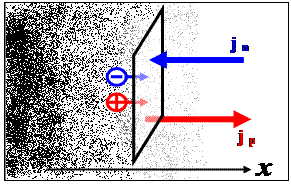
Так как основные носители заряда по обе стороны границы раздела имеют различные знаки, с одной стороны границы раздела возникает градиент концентрации дырок, а с другой электронов. Следовательно возникнет диффузия электронов из n полупроводника в p полупроводник и диффузия дырок из p области в n область, т.е. через границу раздела потечёт диффузионный ток.
Уход основных носителей заряда, в первую очередь из близлежащих к границе раздела областей полупроводников, “оголяет” ионы атомов доноров и акцепторов, положительные в n и отрицательные в p полупроводнике, заряд которых ранее компенсировался основными носителями. Нескомпенсированные объёмные заряды по обе стороны границы раздела полупроводников создают электрическое поле напряжённостью E. Это поле препятствует дальнейшей диффузии основных зарядов, но создаёт возможность дрейфа неосновных носителей заряда – дырок из n области в p область и электронов из p области в n область.
Таким образом, через границу раздела полупроводников текут две составляющие диф-фузионного тока основных носителей заряда, направленные из p области в n область, а также две составляющие дрейфового тока неосновных носителей заряда, направленные из n области в p область. При этом “оголяются” всё более удалённые по обе стороны от границы раздела ионы, т.е. их объёмный заряд растёт.
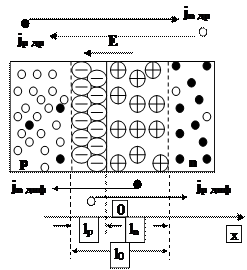Область объёмных зарядов на границе раздела полупроводников разного типа проводимости, обеднённая основными носителями заряда, называетсяp-n переходом.
По мере увеличения объёмного заряда, а следовательно и напряжённости поля E, диффузионный ток уменьшается, а дрейфовый ток возрастает. Этот процесс продолжается до тех пор, пока лишь незначительная часть основных носителей заряда, имеющих энергию, достаточно большую, для преодоления тормозящего действия поля, сможет перемещаться(прорываться) через границу раздела.
Когда диффузионный ток таких носителей заряда уравновесится, растущим по мере увеличения объёмного заряда, током неосновных носителей заряда, наступает состояние динамического равновесия. В этом состоянии токи в смежные области полупроводников уравновешивают друг друга, объёмный заряд перестаёт расти, суммарный ток через границу раздела равен нулю, т.к. внешняя цепь разомкнута.
Итак: jp др + jn др + jp диф + jn диф = 0.
Дата добавления: 2016-05-11; просмотров: 2826;