Полупроводники проводят ток одинаково во всех направлениях.
ФИЗИЧЕСКИЕ ОСНОВЫ ПОЛУПРОВОДНИКОВОЙ ЭЛЕКТРОНИКИ.
2.1. Определяющие свойства полупроводников.
К полупроводникам относятся твёрдые, кристаллические вещества, которые при комнатной температуре (27 ºС =300 ºК) обладают удельным электрическим сопротивлением ρ, лежащим в пределах от (10 -4 ÷10 - 3) Ом ∙ см до (10 8 ÷ 10 10) Ом ∙ см.
Проводники (металлы) обладают значительно меньшим удельным сопротивлением, лежащим в пределах (10 – 6 ÷ 10 - 4 ) Ом ∙ см .
Вещества, имеющие удельное сопротивление порядка ( 10 18 ÷ 10 24 ) Ом ∙ см считаются диэлектриками.
Таким образом полупроводники, по удельной проводимости, занимают промежуточное положение между проводниками и диэлектриками.
Однако, такое разграничение (по удельному сопротивлению) не является исчерпывающим признаком, выделяющим полупроводники в особую группу твёрдых тел. Для полупроводников также характерны следующие отличительные свойства.
а) – Высокая чувствительность их электропроводности к добавлению примесей других веществ даже в незначительных количесвах, (10 - 3 ÷ 10 – 6) объёмного содержания. Например добавление
10 – 5 % примеси в германий – Ge уменьшает его удельное сопротивление в 200 раз.
б) – Сильная, нелинейная, обратная зависимость удельного сопротивления от темперетуры, т.е.
удельное сопротивление полупроводников не растёт с повышением температуры, как у проводников, а наоборот – уменьшается.
в) – Зависимость удельного сопротивления от различного рода излучений – свет, рентгеновское излучение, радиоактивное и т.д.
Совокупность этих (4 – х) признаков достаточно однозначно выделяет полупроводники в особую группу веществ.
Подчеркнём, что удельное сопротивление полупроводников инвариантно к направлению протекающего в них тока.
Полупроводники проводят ток одинаково во всех направлениях.
Наиболее широкое применение в полупроводниковой технике нашли элементы таблицы Менделеева: германий – Ge, кремний – Si, мышьяк – As, галлий – Ga, селен – Se, йод – I, бор – B и др., а также различные соединения: галия с мышьяком – арсенид галлия, закись меди, фосфористый мышьяк и др.
2.2. Собственные полупроводники.
Так, или беспримесными, называются полупроводники, кристаллическая решётка которых состоит из атомов одного вещества, т.е. это химически чистые вещества не содержащие атомов других веществ.
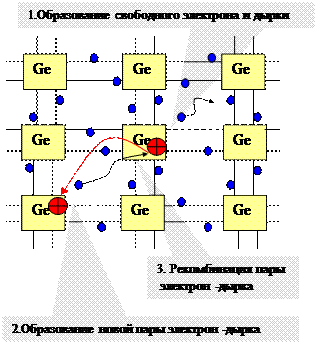 В основе наиболее распространённых полупроводников, например четырёхвалентных германия и кремния, лежит пространственная фигура – тетраэдр, в узлах и центре которой расположены атомы, причём каждый атом окружён четырьмя соседними атомами и связан с ними четырьмя валентными электронами (ковалентные связи). На рис приведён плоский эквивалент фрагмента такой решётки.
В основе наиболее распространённых полупроводников, например четырёхвалентных германия и кремния, лежит пространственная фигура – тетраэдр, в узлах и центре которой расположены атомы, причём каждый атом окружён четырьмя соседними атомами и связан с ними четырьмя валентными электронами (ковалентные связи). На рис приведён плоский эквивалент фрагмента такой решётки.
При температуре абсолютного нуля все ковалентные связи заполнены, все электроны заняты в образовании ковалентных связей, свободных электронов нет и проводимость полупроводника в таком состоянии равна нулю.
При нагревании кристалла атомы в узлах кристаллической решётки начинают совершать хаотические колебательные движения, амплитуда которых увеличивается по мере повышения температуры кристалла.
Энергия этих колебаний передаётся электронам, в результате чего ковалентные связи разрываются и образуются свободные электроны. В отсутствии электрического поля в кристалле они хаотически перемещаются между узлов кристаллической решётки. Одновременно с появлением свободных электронов, атом, потерявший электрон, приобретает положительный заряд. Такой положительный заряд образовавшийся в результате появления дефектной (не занятой электроном или вакантной) связи, называется дыркой. Процесс образования пары электрон - дырка называется генерацией.
Дырка, как показано на рисунке, может хаотически перемещаться в кристалле в результате занятия одним из свободных электронов вакантного места. Процесс исчезновения пар эдектрон – дырка в результате занятия свободным электроном вакантной связи называется рекомбинацией .
Под скоростью процессов генерации и рекомбинации понимают количество пар электрон – дырка, соответственно возникающих и исчезающих в единицу времени.
Скорости генерации и рекомбинации зависят от материала полупроводника, концентрации примесей и температуры, но при любой постоянной температуре скорости этих процессов равны между собой, а при температуре абсолютного нуля (0 ºК) равны нулю.
Таким образом, в отличие от проводников, в полупроводниках имеется два типа подвижных носителей заряда, вектор скорости которых хаотически изменяется по модулю и фазе(направлению). Поэтому, в отсутствии электрического поля, средняя скорость носителей заряда (электронов и дырок) в полупроводнике, в любом выбранном направлении, равна нулю. Отсутствие направленного движения зарядов (по определению электрического тока) означает равенство нулю тока в полупроводнике.
2.3. Энергетические диаграммы собственных полупроводников, проводников и диэлектриков.
Согласно законам классической механики положение орбиты, по которой вокруг ядра атома движется электрон, может быть любым. При этом необходимо равенство центробежной и центростремительной сил: 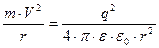 , где m и q – соответственно масса и заряд электрона, V – линейная скорость его движения, r – радиус орбиты.
, где m и q – соответственно масса и заряд электрона, V – линейная скорость его движения, r – радиус орбиты.
Однако в квантовой механике теоретически и экспериментально доказывается, что энергии электронов, а следовательно их орбиты, могут иметь лишь дискретные разрешённые значения, совокупность которых определяет индивидуальные свойства данного вещества, такие как его способность вступать в химические реакции, оптические свойства и т.д..
 Энергетическая диаграмма изолированного атома отображается горизонтальными линями на оси энергий, где каждая линия соответствует разрешённым значениям энергий электронов. Например, для одновалентного атома натрия энергетическая диаграмма выглядит следующим образом. (Здесь, отрицательные значения энергий электронов определяются его отрицательным зарядом).
Энергетическая диаграмма изолированного атома отображается горизонтальными линями на оси энергий, где каждая линия соответствует разрешённым значениям энергий электронов. Например, для одновалентного атома натрия энергетическая диаграмма выглядит следующим образом. (Здесь, отрицательные значения энергий электронов определяются его отрицательным зарядом).
Положения электронов на соответствующих энергетических уровнях характеризуются квантовыми числами, определяющими их орбиты, причём в соответствии с принципом Паули в атоме может быть не более двух электронов, имеющих одинаковые квантовые числа, при условии,что их спины противоположны.
Введём понятие зонной энергетической диаграммы твердого тела, которой мы будем часто пользоваться в дальнейшем, при рассмотрении физических процессов, имеющих место в различных полупроводниковых приборах.
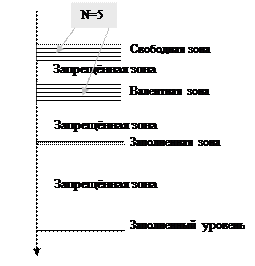 При объединении N атомов в единое твёрдое тело, каждый разрешённый энергетический уровень расщепляется (распадается) на N подуровней, образуя соттветствующие разрешённые энергетические зоны, между которыми располагаются запрещённые зоны. При этом наиболее сильному расщеплению подвергаются энергетические уровни валентной (внешней) электронной оболочки. Так как эта оболочка оказывает экранирующее воздействие на внутренние оболочки, энергетические уровни их электронов распадаются в меньшей степени.
При объединении N атомов в единое твёрдое тело, каждый разрешённый энергетический уровень расщепляется (распадается) на N подуровней, образуя соттветствующие разрешённые энергетические зоны, между которыми располагаются запрещённые зоны. При этом наиболее сильному расщеплению подвергаются энергетические уровни валентной (внешней) электронной оболочки. Так как эта оболочка оказывает экранирующее воздействие на внутренние оболочки, энергетические уровни их электронов распадаются в меньшей степени.
Электропроводность твёрдого тела полностью определяется состояниями электронов валентной и свободной зон, т.к. электроны заполненных зон и уровней жёстко связаны с ядром атома и не могут быт носителями заряда. Поэтому, в дальнейшем, на зонной диаграмме будут изображаться только валентная зона, зона проводимости (свободная зона), и разделяющая их запрещённая зона.
Типичные зонные, энергетические диаграммы собственного полупроводника, при температуре абсолютного нуля и комнатной температуре изображены на рисунках.
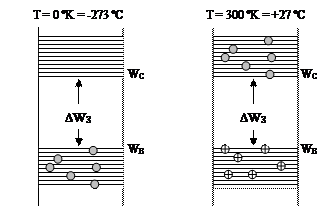 При температуре абсолютного нуля все уровни валентной зоны заполнены (нет дефектных ковалентных связей - дырок), а в свободной зоне нет электронов проводимости. При такой температуре собственный полупроводник ведёт себя как диэлектрик.
При температуре абсолютного нуля все уровни валентной зоны заполнены (нет дефектных ковалентных связей - дырок), а в свободной зоне нет электронов проводимости. При такой температуре собственный полупроводник ведёт себя как диэлектрик.
При повышении температуры полупроводника (облучении) электроны валентной зоны приобретают энергию, достаточную для перехода в зону проводимости.
DWЗ - минимальная энергия, которую надо сообщить валентному электрону, для того чтобы он мог перейти из валентной зоны в зону проводимости. В результате такого перехода, на энергетических уровнях электронов валентной зоны, покинувших её, образуются дырки, а в зоне проводимости свободные электроны. В таком состоянии полупроводник может проводить ток.
Ниже на рисунках приведены энергетические диаграммы проводников (металлов) - а), полупроводников - б) и диэлектриков - в).
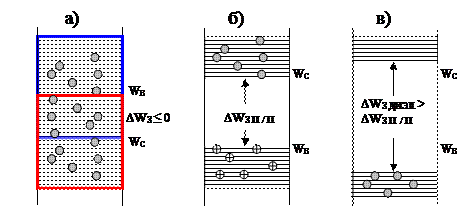 В металлах, при любой температуре валентная и свободная зоны взаимно перекрываются, их электроны являются общими для обеих зон, поэтому, при любой температуре, металлы хорошо проводят ток.
В металлах, при любой температуре валентная и свободная зоны взаимно перекрываются, их электроны являются общими для обеих зон, поэтому, при любой температуре, металлы хорошо проводят ток.
У полупроводников зоны разделены, но даже при комнатной температуре в них образуется достаточно подвижных зарядов, обеспечивающих проводимость.
В диэлектриках ширина запрещённой зоны столь велика, что даже при высокой температуре (вплоть до разрушения материала), сообщаемой энергии недостаточно для переброса электронов из валентной зоны в зону проводимости. Поэтому при любой температуре в диэлектриках нет свободных зарядов, следовательно их проводимость теоретически равна нулю.
2.4. Проводимость полупроводников.
Если создать в полупроводнике статическое электрическое поле E, подключив к нему источник постоянного напряжения U, то к хаотической составляющей скорости электронов и дырок добавится регулярная составляющая скорости, направленная вдоль линий поля E.
Средняя, приобретённая скорость электронов и дырок соответственно равна :
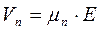 и
и 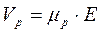 .
.
Здесь 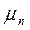 и
и 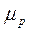 - соответственно подвижности электронов и дырок физический смысл которых легко уяснить, выразив их из приведённых выше фомул:
- соответственно подвижности электронов и дырок физический смысл которых легко уяснить, выразив их из приведённых выше фомул:
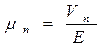 ,
, 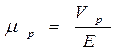 и приняв
и приняв 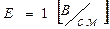 .
.
Тогда: 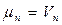 и
и 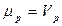 т.е. подвижность носителей заряда есть средняя скорость, приобретаемая ими в электрическом поле напряжённостью 1 [В / см].
т.е. подвижность носителей заряда есть средняя скорость, приобретаемая ими в электрическом поле напряжённостью 1 [В / см].
| Типичные значения подвижности зарядов для германия и кремния при комнатной температуре (300ºК=27ºС). | ||
| Ge | Si | |
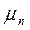 [см/сек.] [см/сек.]
| ||
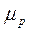 [см/сек.] [см/сек.]
|
Подвижность носителей заряда зависит от вещества, из которого изготовлен полупроводник, типа кристаллической решётки, количества примесей и температуры и в значительной мере определяет быстродействие полупроводниковых приборов (их способность работать на высоких частотах напряжений и токов).
Наибольшей подвижностью обладают заряды в германие и кремние, что обусловило их широкое применение в качестве исходных материалов для изготовления полупроводниковых приборов.
Определим проводимость полупроводника.

| |
| |
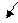
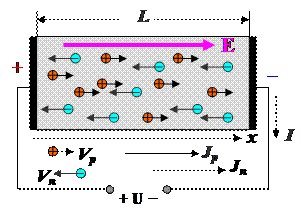 Пусть площадь сечения образца полупроводника, изображённого на рисунке равна
Пусть площадь сечения образца полупроводника, изображённого на рисунке равна 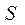 . Полное сопротивление образца полупроводника между контактами 1 и 2
. Полное сопротивление образца полупроводника между контактами 1 и 2 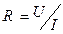 ,
,
Удельное сопротивление материала 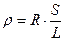 , а его удельная проводимость
, а его удельная проводимость 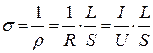 .
.
Так как 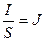 - полной плотности тока, а
- полной плотности тока, а
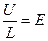 - напряжённость поля в полупроводнике, удельную проводимость образца полупроводника можно представить в виде:
- напряжённость поля в полупроводнике, удельную проводимость образца полупроводника можно представить в виде: 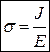 .
.
Полная плотность тока в полупроводнике 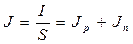 ,
,
где 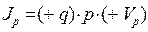 - плотность дырочной составляющей полного тока,
- плотность дырочной составляющей полного тока,
а 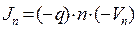 - плотность электронной составляющей.
- плотность электронной составляющей.
Здесь ( + q ) и (− q) – соответственно заряд дырки и электрона равные по абсолютной величине (потеря нейтральным атомом отрицательного заряда q, приводит к появлению положительного нескомпенсированного заряда ядра атома с таким же абсолютным значением),
pи n - концентраций, соттветвтвенно электронов и дырок, а Vp и Vn - модули векторов приобретенной направленной скорости дырок и электронов. При этом за положительное направление тока в полупроводнике принято направление, совпадающее с направлением оси х, изображённой на рисунке.
Заметим, что разные знаки зарядов и противоположное направление их движения обусловливают совпадение направлений создаваемых ими токов.
Подставив в выражение для плотности полного тока значения модулей скорости дырок 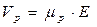 и скорости электронов
и скорости электронов 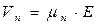 , получим :
, получим :
.
Поделив обе части этого выражения на Е, получим: 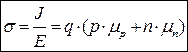 . Отметим, что
. Отметим, что
это выражение получено безотносительно к типу полупроводника и является общим как для собственных, так и для примесных полупроводников, структура и проводимость которых будут рассмотрены несколько позже.
2.5. Электропроводность собственных полупроводников.
Так как при любой постоянной температуре скорости генерации и рекомбинации равны между собой, а при температуре абсолютного нуля (0 ºК) равны нулю, то в собственном полупроводнике 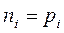 .
.
. Тогда 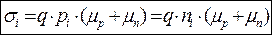 . Здесь и далеее индекс i означает собственный полупроводник.
. Здесь и далеее индекс i означает собственный полупроводник.
Чтобы при заданной, постоянной температуре определить проводимость собственного полупроводника надо знать концентрацию носителей заряда ni (заряд электрона q = 16 ∙ 10-20 Кулон, а подвижности носителей заряда mn и mp являются априорно определёнными справочными величинами).
Из за того, что при температуре отличной от нуля по Кельвину, узлы кристаллической решётки испытывают хаотические колебания, говорить о том, что валентный электрон, имеющий в данный момент времени некоторую энергию, получит её приращение имеющее заранее известное (детерминированное) значение, не имеет смысла. Поэтому судить о том, сколько электронов, при данной температуре полупроводника, будет в состоянии покинуть валентную зону и оказаться в зоне проводимости, можно лишь вероятностно.
Вероятность заполнения электроном энергетического уровня с энергией W, при заданной температуре T, количественно выражается функцией распределения Ферми-Дирака:
Fn(W) = 1/(1 + exp((W - WF) / kT ))
где k – постоянная Больцмана, T – абсолютная температура. WF – носит название уровня Ферми.
Очевидно, что могут иметь место лишь два события – либо данный энергетический уровень занят электроном, либо не занят ( т.е. он занят дыркой). Эти два события составляют полную группу, следовательно если обозначить через Fp(W) вероятность нахождения дырки на энергетическом уровне W, то можем записать Fn(W) + Fp(W) = 1. Т.е. Fp(W) = 1 - Fn(W), или Fp(W) = 1/(1 + exp((WF - W) / kT )).
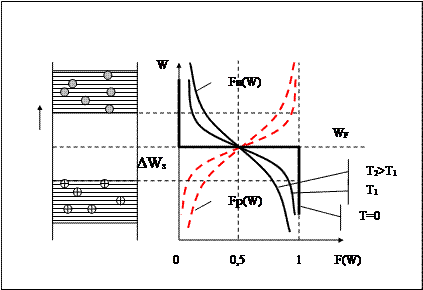 Величина WF, входящая в выражение, называется энергией или уровнем Ферми, который может быть определён как энергетический уровень равновероятный как для электрона, так и для дырки.
Величина WF, входящая в выражение, называется энергией или уровнем Ферми, который может быть определён как энергетический уровень равновероятный как для электрона, так и для дырки.
При T=0 функция Ферми превращается в ступенчатую.
Дата добавления: 2016-05-11; просмотров: 3046;
