ПОЯСНИТЬ ХОД КРИВЫХ !!!
Для собственного полупроводника уровень Ферми лежит в середине запрещённой зоны, т.к. функция вероятности симметрична относительно него при любой фиксированной температуре.
Заметим, что функция Ферми имеет
смысл только в валентной и запрещённой зонах, т.к. в запрещённой зоне носители заряда находиться не могут. Воспользуемся статистикой Ферми-Дирака для определения концентрации электронов и дырок в собственном полупроводнике. Учтём, что энергетические уровни зоны проводимости, а также и валентной зоны распределены неравномерно, т.е. их плотность зависит от энергии.
Число энергетических уровней в зоне проводимости, попадающих в единичный, бесконечно малый энергетический интервал dW, обозначим через функцией P(W), которая будет характеризовать плотность энергетических уровней. Тогда количество электронов, занимающих разрешённые энергетические уровни в некоторой полосе dW определяется числом уровней dW·P(W) в этой элементарной полосе и вероятностью их заполнения Fn(W)
т.е dni = P(W)·Fn(W)·dW.
Полное число электронов, приходящихся на 1 см3 вещества и занимающих энергетические уровни в полосе энергий от W1 до W2 будет равно:
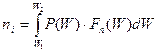
Аналогичным образом для концентрации дырок валентной зоны получим:
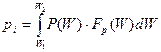
В обоих случаях интегрирование ведётся по всей ширине зоны проводимости (сonductivity) или валентной (valency) зоны. В результате интегрирования можно придти к следующим выражениям:
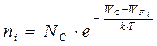
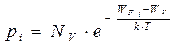 .
.
Здесь 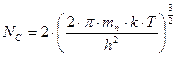 , а
, а 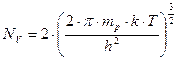
NС и NV- эффективная плотность состояний (на 1 см3) в зоне проводимости и валентной зоне
соответственно.
h = 4,14·10-15 эв·сек – постоянная Планка. mn и mp – эффективная масса электрона и дырки соответственно.
* Эффективная масса электрона определяется из уравнения F = mn ·dV/dt, где F – кулоновская сила, действующая на электрон, а V – скорость электрона.
В большинстве практических случаев можно считать, что mn = mp = m – массе электрона в состоянии покоя. Тогда:
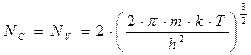
 Положив далее, что ΔWз = Wc -Wv и учитывая, что в собственном полупроводнике ni = pi , выражения для концентрации электронов и дырок можно привести к виду:
Положив далее, что ΔWз = Wc -Wv и учитывая, что в собственном полупроводнике ni = pi , выражения для концентрации электронов и дырок можно привести к виду:
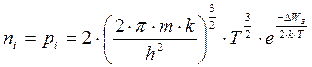
При этих условиях уровень Ферми лежит точно посередине запрещённой зоны,
т.е. WFi = (Wс-Wv) / 2.
Подставляя найденное значение концентрации ni в выражение для проводимости собственного полупроводника придем к следующей зависимости: 
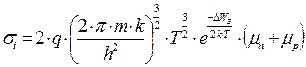 .
.
Или 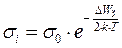 где
где 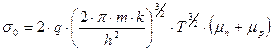
Как правило ΔWЗ >> k·T, подвижности зарядов μn и μp мало зависят от температуры, а экспонента растёт гораздо быстрее, чем T 3/2 . Поэтому, с достаточной для практики точностью, можно считать, что определяющее влияние на зависимость 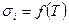 оказывает экспонента
оказывает экспонента 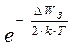 , а не множители T 3/2 и (μn + μp),т.е принять
, а не множители T 3/2 и (μn + μp),т.е принять
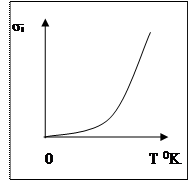 σ 0 = const.
σ 0 = const.
Из последних выражений и рисунка видно, что зависимость удельной проводимости собственного полупроводника от температуры носит сугубо нелинейный характер и близка к экспоненциальной.
2.6. Примесные полупроводники.
2.6.1. Полупроводник типа – n или электронного типа.
Электропроводность полупроводников может быть существенно увеличена путём добавления незначительного количества примесей. Так на электропроводность таких полупроводников, как германий и кремний особенно большое влияние оказывают примеси трёхвалентных элементов алюминия, бора, галлия, индия, а также пятивалентные примеси фосфора, мышьяка, сурьмы.
Если в идеальный кристалл полупроводника ввести примесь пятивалентного мышьяка, то его атомы замещают атомы основного вещества в узлах кристаллической решётки. При этом четыре валентных электрона атома мышьяка вступят в связь с четырьмя электронами соседних атомов германия. Пятый электрон в связи не участвует и поэтому слабо связан со своим материнским атомом. При температуре отличной от нуля он оторван от ядра и может свободно перемещаться в
узлах кристаллической решётки. Энергия ионизации такого атома равна всего лишь
ΔWион. = 0,012 эв.
 Такой электрон называется свободным электроном. Отрыв электрона от атома превращает его в положительный ион, неподвижно закреплённый в узлах кристаллической решётки. Такой ион не является носителем заряда, он неподвижен – это не дырка. Не путать! Увеличивая концентрацию примеси можно легко получить концентрацию электронов, на несколько порядков превышающую концентрацию дырок, обусловленную процессами термогенерации пар электрон - дырка. В таком полупроводнике основными носителями заряда являются электроны, а дырки неосновными носителями заряда т.к. дырочный ток выражен слабо. Поэтому такой полупроводник называется электронным или полупроводником типа n. Примеси отдающие лишний электрон и обусловливающие электронную проводимость называются донорными. Процесс введения примеси в полупроводник называется легированием, а примесный полупроводник - легированным.
Такой электрон называется свободным электроном. Отрыв электрона от атома превращает его в положительный ион, неподвижно закреплённый в узлах кристаллической решётки. Такой ион не является носителем заряда, он неподвижен – это не дырка. Не путать! Увеличивая концентрацию примеси можно легко получить концентрацию электронов, на несколько порядков превышающую концентрацию дырок, обусловленную процессами термогенерации пар электрон - дырка. В таком полупроводнике основными носителями заряда являются электроны, а дырки неосновными носителями заряда т.к. дырочный ток выражен слабо. Поэтому такой полупроводник называется электронным или полупроводником типа n. Примеси отдающие лишний электрон и обусловливающие электронную проводимость называются донорными. Процесс введения примеси в полупроводник называется легированием, а примесный полупроводник - легированным.
На зонной модели появление свободных электронов означает, что энергетические уровни атомов доноров располагаются в запрещённой зоне вблизи дна зоны проводимости основного материала полупроводника. Отметим, что количество примесных атомов на единицу объёма, на несколько порядков меньше количества атомов основного полупроводника. Поэтому атомы примеси располагаются на значительных расстояниях друг от друга и расщепления энергетических уровней атомов примеси (доноров) практически не происходит. Уровень Ферми на энергетической диаграмме смещается к зоне проводимости. При температуре близкой к абсолютному нулю все донорные уровни оказываются занятыми. Но уже при незначительном повышении температуры, электроны, находящиеся на донорных уровнях, получают энергию, достаточную для перехода в зону проводимости. Донорные уровни при этом освобождаются, образуются ионы атомов примеси.
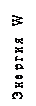
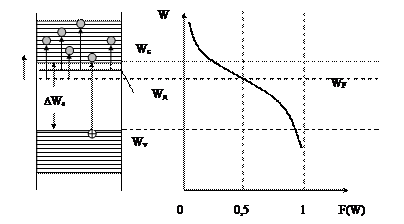 Концентрации электронов и дырок в полупроводнике типа n рассчитываются также на основе статистики Ферми-Дирака.
Концентрации электронов и дырок в полупроводнике типа n рассчитываются также на основе статистики Ферми-Дирака.
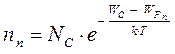 - для электронов,
- для электронов, 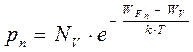 - для дырок,
- для дырок,
где WFn – уровень Ферми в полупроводнике типа n, определяемый выражением
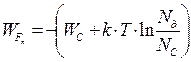
Дата добавления: 2016-05-11; просмотров: 1371;
