Уравнение непрерывности заряда является выражением общего закона неопределённости в физике.
Его физический смысл состоит в том, что заряды в некоторой области не могут возникать или исчезать за бесконечно короткие промежутки времени, т.к. на это требуется бесконечно большая энергия.
Применительно к решаемой нами задаче, для идеализированного перехода уравнение непрерывности приводится к следующим выражениям, которые называются уравнениями диффузии: 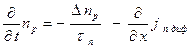
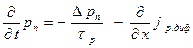 .
.
Для количественного определения токов через p – n переход уравнения диффузии для электронов и дырок соответственно, решаются совместно с приведёнными ранее уравнениями плотности токов. jn диф. = q·Dn·∂ np/∂x , jp диф. = -q·Dp·∂ pn/∂x , где: Dn и Dp – коэффициенты диффузии, Δ np и Δ pn – граничные концентрации, τn и τp – время жизни электронов и дырок соответственно, т.е. время, в течение которого концентрация соответствующих носителей заряда уменьшается в е раз, x – расстояние, отсчитываемое от границы p-n перехода вглубь области электронного или дырочного полупроводника.
 Окончательное решение этих уравнений имеет вид:
Окончательное решение этих уравнений имеет вид:
для x>0,
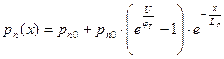
для x <0.
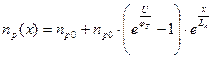 ,
,
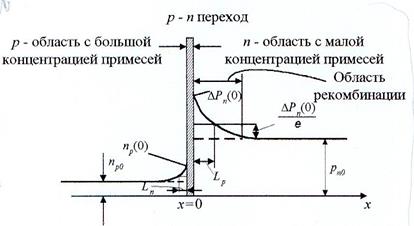
Здесь: Ln и Lp – диффузионная длина электронов и дырок соответственно, т.е. расстояние, на котором соответствующая концентрация в результате рекомбинации убывает в e раз по сравнению с её граничным значением Δn(x) или Δp(x).
Диффузионная длина, время жизни и коэффициенты диффузии связаны соотношениями:
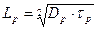 и
и 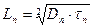
Подставляя выражения для концентраций в уравнения плотности токов, получим:
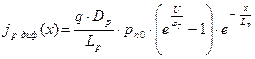 ,
, 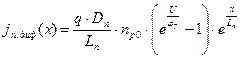 .
.
Хотя, как следует из этих выражений, jn диф и jp диф зависят от x, общий ток p-n перехода постоянен в любом сечении полупроводника. Вблизи границ перехода, при x=0, этот ток практически диффузионный, поэтому он может быть найден как сумма j диф = jn диф + jp диф при x=0.
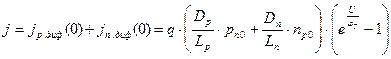 .
.
Соответственно, ток I через p-n переход площадью S равен I = j · S .
Подставив в эту формулу найденное значение плотности тока, получим:
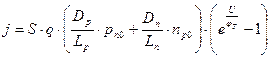 .
.
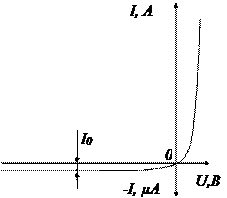 Как это следует из выражения, ток I через p-n переход является экспоненциальной функцией приложенного к нему напряжения U и температуры T (φT = k·T/q). Кроме того, при U = const, величина тока определяется параметрами S, Dn, Dp, Ln, Lp, pn0, np0, характеризующими геометрию перехода, материал полупроводников, концентрацию неосновных носителей, а значит концентрацию примесей (степень легирования). Поэтому коэффициент при экспоненте удобно выделить, обозначив его как I 0.
Как это следует из выражения, ток I через p-n переход является экспоненциальной функцией приложенного к нему напряжения U и температуры T (φT = k·T/q). Кроме того, при U = const, величина тока определяется параметрами S, Dn, Dp, Ln, Lp, pn0, np0, характеризующими геометрию перехода, материал полупроводников, концентрацию неосновных носителей, а значит концентрацию примесей (степень легирования). Поэтому коэффициент при экспоненте удобно выделить, обозначив его как I 0.
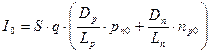 .
.
Тогда ток I через p-n переход 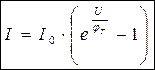 .
.
|
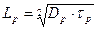 и
и 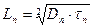 получим:
получим:
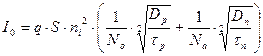 . Поскольку,
. Поскольку, 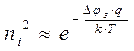 где Δφз – ширина запрещённой зоны, то 1) - этот ток будет сильно зависеть от температуры, поэтому его часто называют тепловым. 2) – этот ток будет тем меньше, чем больше ширина запрещённой зоны Δφз .
где Δφз – ширина запрещённой зоны, то 1) - этот ток будет сильно зависеть от температуры, поэтому его часто называют тепловым. 2) – этот ток будет тем меньше, чем больше ширина запрещённой зоны Δφз .
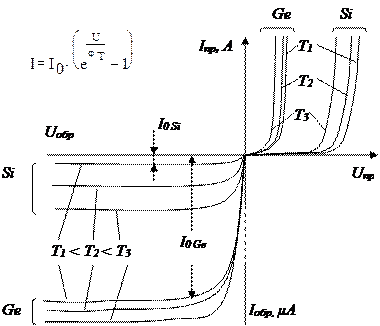 Например, у кремния ширина запрещённой зоны Δφз = 1,12В, а у германия Δφз = 0,66В. Поэтому абсолютное значение теплового тока кремниевого перехода на несколько порядков меньше соответствующего тока германиевого перехода. Однако, по той же причине, относительное изменение теплового тока кремниевого перехода значительно больше чем у германиевого. В этом можно убедиться взяв производную d n i /d T .
Например, у кремния ширина запрещённой зоны Δφз = 1,12В, а у германия Δφз = 0,66В. Поэтому абсолютное значение теплового тока кремниевого перехода на несколько порядков меньше соответствующего тока германиевого перехода. Однако, по той же причине, относительное изменение теплового тока кремниевого перехода значительно больше чем у германиевого. В этом можно убедиться взяв производную d n i /d T .
На рисунке дано качественное сравнение вольтамперных характеристик германиевого и кремниевого переходов, при различных температурах. Прямая ветвь вольтамперной характеристики кремниевого перехода как бы сдвинута вправо (обычно на 0,3 – 0,4В) относительно ВАХ германиевого перехода, т.к. величина I 0, входящая масштабным множителем в выражение для тока, у кремниевых переходов на несколько порядков меньше, чем у германиевых. По той же причине обратный ток в кремниевом переходе на несколько порядков меньше, чем у германиевого. Как прямой, так и обратный токи p-n перехода возрастают с увеличением температуры, причём относительное изменение тока у кремниевого перехода выражено сильнее.
3.5. Вольтмперная характеристика реального p-n перехода.

Вольтамперная характеристика реального диода отличается от теоретической ВАХ идеализированного перехода. Расхождение в обратных ветвях связано, во-первых наличием поверхностного тока утечки Iут, который растёт пропорционально обратному напряжению. Во-вторых, величина обратного тока в реальном переходе увеличивается за счёт термотока IT, обусловленного процессом генерации носителей заряда в самом p-n переходе, который не учитывался при выводе ВАХ. С ростом обратного напряжения термоток растёт пропорционально 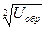 .
.
На ход прямой ветви оказывает влияние сопротивление объёмов полупроводников по обе стороны p-n перехода, которым мы пренебрегли. Особенно сильное влияние оказывает область базы, т.е. область с меньшей степенью легирования. Прямой ток создаёт на базе падение напряжения Uб = I · rб. Поэтому напряжение, действующее непосредственно на переходе будет U - I · rб .
3.6. Характеристические сопротивления p-n перехода.
 Свойства p-n перехода количественно можно охарактеризовать его сопротивлением постоянному и переменному току. Соответственно R 0 = U / I – сопротивление постоянному току, а R д = dU / dI – дифференциальное сопротивление или сопротивление переменному току достаточно малой амплитуды. Вследствие нелинейности ВАХ перехода, R 0 и R д имеют значительно меньшие значения на прямой ветви чем на обратной. С другой стороны всегда R 0 > R д в области прямых токов, а в области обратных токов R 0 < R д . Отметим, что обе эти величины являются функциями напряжения или тока R 0 = f(U) или R 0 = f(I) и R д = f (U) или R д = f (I), т.е. значения этих величин зависят от положения точки на ВАХ в которой они были определены.
Свойства p-n перехода количественно можно охарактеризовать его сопротивлением постоянному и переменному току. Соответственно R 0 = U / I – сопротивление постоянному току, а R д = dU / dI – дифференциальное сопротивление или сопротивление переменному току достаточно малой амплитуды. Вследствие нелинейности ВАХ перехода, R 0 и R д имеют значительно меньшие значения на прямой ветви чем на обратной. С другой стороны всегда R 0 > R д в области прямых токов, а в области обратных токов R 0 < R д . Отметим, что обе эти величины являются функциями напряжения или тока R 0 = f(U) или R 0 = f(I) и R д = f (U) или R д = f (I), т.е. значения этих величин зависят от положения точки на ВАХ в которой они были определены.
3.7. Емкостные свойства p-n перехода.
Так как процессы, происходящие в p-n переходе при изменении напряжения на нём, связаны с перемещением и изменением зарядов, следует ожидать проявления емкостных свойств перехода в целом. Различают два типа емкостных характеристик, присущих p-n переходу.
3.7.1. Барьерная или зарядная емкость p-n перехода.
Так как область объёмного заряда в переходе, представляет собой двойной слой противоположных по знаку неподвижных зарядов, а толща полупроводника по обе стороны перехода обладает достаточно хорошей проводимостью, то в целом такой p-n переход можно представить как плоский конденсатор, ёмкость которого рассчитывается по формуле
Cбар = dQ/dU = ε·ε0·S / l .
Поскольку ширина перехода зависит от приложенного напряжения U, то и емкость будет зависеть от напряжения U .
Для ступенчатого перехода 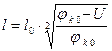 , а
, а 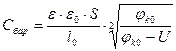
3.7.2. Диффузионная ёмкость p-n перехода.
При прямом смещении перехода в p и n областях за счёт инжекции происходит накопление подвижных неравновесных носителей заряда. Отношение изменения инжектированного заряда к изменению напряжения на переходе определяет диффузионную ёмкость p-n перехода
Cдиф = dQинж / dU. С учётом инжекции в обе стороны p-n перехода
Сдиф = q(I p· τp + I n· τn) / k·T ,
где In и Ip – электронная и дырочная составляющие прямого тока. Отсюда следует, что диффузионная ёмкость пропорциональна прямому току и может достигать больших значений. Полная ёмкость p-n перехода Cпер= Сбар + Сдиф .
Наличие емкости приводит к нежелательным фазовым сдвигам между напряжением на p-n перехо де и током, протекающим через него, при работе приборов на переменном токе.
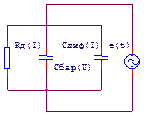
Эквивалентную схему p-n перехода при работе на малых значениях токов и напряжений можно представить в след. виде. Заметим, что параметры эквивалентной схемы зависят от постоянного смещения
на переходе. Наличие емкостей ухудшает выпрямительные свойства перехода с ростом частоты переменного напряжения.
Однако именно благодаря наличию зависимой от напряжения барьерной емкости перехода, появилась возможность создания специальных приборов, которые мы рассмотрим чуть позже.
3.8. Пробой p-n перехода. Виды пробоя переходов.
Под пробоем p-n перехода обычно понимают резкое увеличение обратного тока Iобр при увеличении обратного напряжения Uобр до некоторого значения Uпроб, называемого напряжением пробоя.
В зависимости от процессов, имеющих при этом место, пробой перехода может быть обратимым или необратимым.
Обратимым называют такой пробой перехода, когда после устранения причины его вызвавшей, т.е. уменьшения обратного напряжения, происходит резкое уменьшение обратного тока до прежнего значения. При этом не происходит никаких изменений в кристаллической структуре материалов, образующих p-n переход. Обратимый пробой может повторяться сколь угодно раз в процессе эксплуатации прибора.
Необратимым считается пробой приводящий к разрушению кристаллической структуры перехода, когда после уменьшения обратного напряжения обратный ток остаётся большим, при этом свойства перехода не восстанавливаются, прибор приходит в негодность.
Различают три основных механизма пробоя: туннельный (зенеровский или полевой), лавинный и тепловой.
3.8.1. Туннельный пробой.
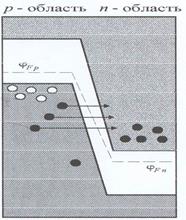
Сущность туннельного эффекта состоит в том, что при большой напряжённости поля, когда энергетические зоны соседних областей занимают положение показанное на рисунке, электроны валентной зоны p-области могут без изменения своей энергии переходить на валентные уровни n-области. Туннельный пробой обычно начинается при напряжённости поля 2·107 В/м для германия и 2·108 для кремния.
Такая высокая напряжённость поля характерна для узких переходов, т.е. для полупроводников с высокой степенью легирования.
Туннельный пробой носит обратимый характер и широко используется для создания полупроводниковых приборов основанных на этом эффекте.
3.8.2. Лавинный пробой.
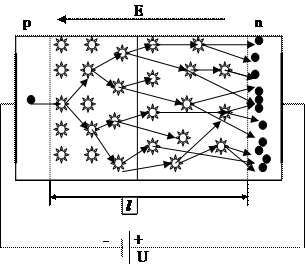 Лавинный пробой развивается в p-n переходах образованных слаболегированными полупроводниками, когда ширина перехода достаточно велика. При лавинном пробое носители в p-n переходе разгоняясь до больших скоростей приобретают высокую энергию, достаточную для ударной ионизации атомов кристаллической решётки. Высвободившиеся при этом электроны, также приобретая большие энергии, ионизируют всё большее число атомов в переходе. При некотором значении напряжения этот процесс переходит в лавинообразный. Происходит резкое увеличение обратного тока – пробой перехода. Также как и туннельный лавинный пробой носит обратимый характер и также используется для создания различных п/п приборов.
Лавинный пробой развивается в p-n переходах образованных слаболегированными полупроводниками, когда ширина перехода достаточно велика. При лавинном пробое носители в p-n переходе разгоняясь до больших скоростей приобретают высокую энергию, достаточную для ударной ионизации атомов кристаллической решётки. Высвободившиеся при этом электроны, также приобретая большие энергии, ионизируют всё большее число атомов в переходе. При некотором значении напряжения этот процесс переходит в лавинообразный. Происходит резкое увеличение обратного тока – пробой перехода. Также как и туннельный лавинный пробой носит обратимый характер и также используется для создания различных п/п приборов.
3.8.3. Тепловой пробой.
 Этот вид пробоя p-n перехода наступает в том случае, если количество тепла, выделяющегося в переходе в единицу времени, пропорциональное мощности рассеиваемой на переходе, становится больше количества тепла отводимого от p-n перехода в единицу времени. В этом случае температура перехода растёт, что приводит к увеличению концентрации неосновных носителей заряда, а следовательно к увеличению обратного тока и ещё большему разогреву перехода. Температура и ток лавинно нарастают, причем при повышенной температуре большие значения тока могут иметь место при меньших напряжениях на переходе, чем то напряжение при котором началось резкое увеличение тока, т.е. напряжение пробоя.
Этот вид пробоя p-n перехода наступает в том случае, если количество тепла, выделяющегося в переходе в единицу времени, пропорциональное мощности рассеиваемой на переходе, становится больше количества тепла отводимого от p-n перехода в единицу времени. В этом случае температура перехода растёт, что приводит к увеличению концентрации неосновных носителей заряда, а следовательно к увеличению обратного тока и ещё большему разогреву перехода. Температура и ток лавинно нарастают, причем при повышенной температуре большие значения тока могут иметь место при меньших напряжениях на переходе, чем то напряжение при котором началось резкое увеличение тока, т.е. напряжение пробоя.
Pрас = Uобр · Iобр Pотв = (Тпер – Tокр) / R T , где Pрас – мощность рассеиваемая на переходе, Pотв – мощность отводимая от перехода, Тпер – температура p-n перехода, Tокр- температура окружающей среды, R T- тепловое сопротивление.
Германиевым переходам более присущ тепловой пробой из-за свойственного им большого обратного тока, т.е. в таких приборах тепловой пробой наступает при меньших значениях обратного напряжения, чем туннельный или лавинный пробой. Для кремниевых приборов характерным является туннельный или лавинный пробой, в зависимости от степени легирования. Тепловой пробой в кремниевых приборах обычно развивается в результате разогрева перехода при туннельном или лавинном пробое, в условиях недостаточного теплоотвода.
Дата добавления: 2016-05-11; просмотров: 1280;
