Сложение взаимно перпендикулярных колебаний

Рассмотрим результат сложения двух гармонических колебаний одинаковой час­тоты w, происходящих во взаимно перпен-дикулярных направлениях вдоль осей х и y.

Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем

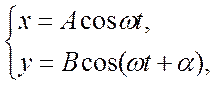(18.37)

где a - разность фаз обоих колебаний, A и В - амплитуды складываемых колебаний.

Уравнение траектории результирующего колебания находится исключением из выра-жений (18.37) параметра t. Записывая склады-ваемые колебания в виде

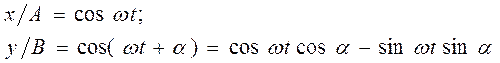
и заменяя во втором уравнении coswt на х/А и sinwt на 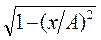,получим после несложных преобразований уравнение эллипса, оси кото-рого ориентированы относительно координат-ных осей произвольно:

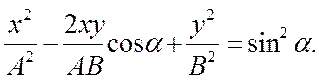(18.38)

Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.

Ориентация эллипса и размеры его осей зависят от амплитуд складываемых колебаний и разности фаз a. Рассмотрим некоторые частные случаи, представляющие физический интерес:

1) a=mp (m=0, ±1, ±2, ...). В данном случае эллипс вырождается в отрезок прямой

у=±(В/А)х, (18.39)

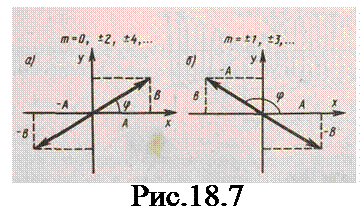где знак плюс соответствует нулю и четным значениям т (рис.18.7,а),

а знак минус - нечетным значениям т (рис.18.7,б). Результирующее колебание является гармоническим колебанием с частотой w и амплитудой 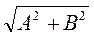,совершаю-щимся вдоль прямой (18.39), составляющей с осью х угол 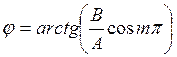. В данном случае имеем дело с линейно поляризованными колебаниями;

2) a=(2m+1)p/2 (m=0, ±1, ±2, ...). В данном случае уравнение примет вид

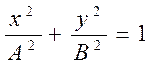. (18.40)

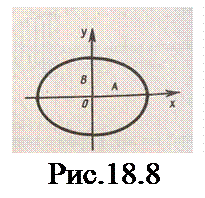Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис.18.8). Кроме того, если А=В, то эллипс (18.40) вырождается в окружность. Такие колебания называются циркулярно поляризо­ванны-ми колебаниямиили колеба-ниями, поляризованными по кругу.

Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые тра­ек-тории, прочерчиваемые точкой, совершаю-щей одновременно два взаимно перпендику-лярных колебания, называются фигурами Лиссажу(Ж. Лиссажу (1822—1880) - французский физик). Вид этих кривых зависит от амплитуд, частот и разности фаз склады-ваемых колебаний. На рис.18.9 представлены фигуры Лиссажу для различных соотношений частот (указаны слева) и разностей фаз (указаны вверху; разность фаз принимается равной j).

Отношение частот складываемых колеба-ний равно отношению числа пересечений фигур Лиссажу с прямыми, параллельными осям координат. По виду фигур можно определить неизвестную частоту по известной или определить отношение частот складывае-мых колебаний. Поэтому анализ фигур Лиссажу - широко используемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.

18.7. Свободные затухающие колебания
Автоколебания

Рассмотрим свободные затухающие коле-бания- колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются.

Простейшим механизмом уменьшения энергии колебаний является её превращение в теплоту вследствие трения в механических колебательных системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.

Закон затухания колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы - идеали-зированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса изменяются. Линейными системами являются, например, пружинный маятник при малых растяжениях пружины (когда справедлив закон Гука), колебательный контур, индуктивность, емкость и сопротивление которого не зависят ни от тока в контуре, ни от напряжения. Различные по своей природе линейные системы описываются идентич-ными линейными дифференциальными урав-нениями. Это позволяет подходить к изуче­нию колебаний различной физической природы с единой точки зрения, а также проводить их моделирование, в том числе и на ЭВМ.

Дифференциальное уравнение свобод-ных затухающие колебали линейной систе-мы задается в виде

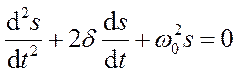, (18.41)

где s - колеблющаяся величина, описывающая тот или иной физический процесс, d = const - коэффициент затухания, w₀— циклическая (угловая) частота свободных незатуха­ющих колебаний той же колебательной системы, т.е. при d =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение уравнения (18.41) в случае малых затуханий (d ²<<w₀²) имеет вид

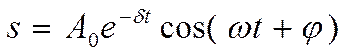, (18.42)

где

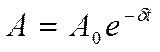(18.43)

- амплитуда затухающих колебаний, а А₀- начальная амплитуда. Зависимость (18.42) показана на рис.18.10 сплошной линией, а зависимость (18.43) – штриховыми линиями.

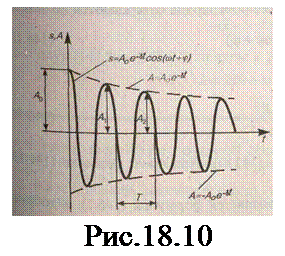Промежуток времени t=1/d, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации. Затухание нарушает периодичность колеба-ний, поэтому затухающие колебания неявля-ются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то мо-жно условно пользоваться понятием периода как промежутка времени между двумя после-дующими максимумами (или минимумами) колеблющейся физической величины (рис.18.10). Тогда период затухающих колебаний будет равен

.

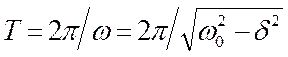Если А(t)и А(t+Т )- амплитуды двух после-довательных колебаний, соответст­вующих моментам времени, отличающимся на период, то отношение

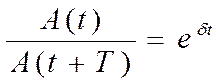
называется декрементом затухания, а его логарифм

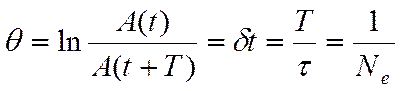(18.44)

- логарифмическим декрементом затуха-ния; N_e — число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания - по­с-тоянная для данной колебательной системы величина.

Для характеристики колебательной системы пользуются понятием добротность Q, которая при малых значениях логарифмического декремента равна

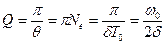(18.44)

(так как затухание мало (d²<<w₀²), то T принято равным T₀).

Из формулы (18.44) следует, что добротность пропорциональна числу колебании N_e,совершаемых системой за время релаксации.

Выводы, полученные для свободных зату-хающих колебаний линейных систем, приме-нимы для колебаний различной физической природы - механических, электромагнитных и др.

В заключение отметим, что при увеличе-нии коэффициента затухания d период зату-хающих колебаний растет и при d=w₀ обра-щается в бесконечность, т.е. движение перес-тает быть периодическим и колебательным. Такой процесс называется апериодическим.

Существуют также так называемые авто­колебания - незатухающие колебания, под-держиваемые в системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний опре­деляются самой систе-мой.

Автоколебания принципиально отличаются от свободных незатухающих колебаний, происходящих без действия сил, а также от вынужденных колебаний, происходящих под действием периодической силы.

Примером автоколебательной системы могут служить часы. Храповой механизм подталкивает маятник в такт с его колебаниями. Энергия, передаваемая при этом маятнику, берется либо за счет раскручивающейся пружины, либо за счет опуска­ющегося груза. Автоколебательными системами являются также двигатели внутреннего сгорания, паровые турбины, ламповый генератор и т. д.