Взаимное положение двух прямых
Две прямые в пространстве могут пересекаться, быть параллельными или скрещиваться.
Если прямые а и b пересекаются в некоторой точке K, то на основании свойства принадлежности точки прямой линии проекции К1 и К2 точки К должны принадлежать одноименным проекциям прямых а и b в соответствии с рисунком 1.3.9.
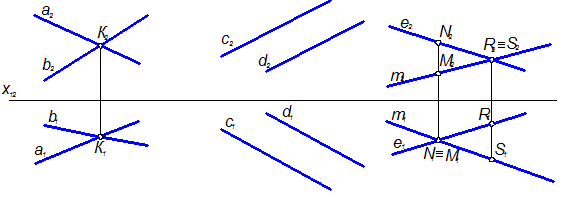 |
Рисунок 1.3.9 – Взаимное положение двух прямых
Иначе говоря, точки пересечения одноименных проекций двух пересекающихся прямых лежат на одной и той же линии связи.
Если прямые с и d параллельны, то на основании свойства параллельности одноименные проекции параллельных прямых также параллельны, т.е. c1||d1 и c2||d2 в соответствии с рисунком 1.3.9.
Если прямые e и m скрещиваются и их одноименные проекции соответственно пересекаются в точках M1ºN1 и R2ºS2, то эти точки не должны лежать на одной линии связи (рисунок 1.3.9), так как в противном случае прямые e и m пересекались бы. Следует заметить, что точки М и N являются горизонтально конкурирующими, а точки R и S – фронтально конкурирующими.
Если прямые являются профильными, то для определения взаимного положения прямых необходимо построить профильные проекции этих прямых.
Например, рассматривая двухкартинный комплексный чертёж (на П2 и П1) прямых АВ и СD (рисунок 1.3.10), можно ошибочно сделать заключение, что они параллельны. В действительности прямые скрещиваются, что очевидно после построения профильной проекции. В случае, когда только одна из прямых занимает профильное положение, для определения взаимного положения прямых кроме построения профильной проекции можно использовать метод пропорционального деления отрезка: если прямые пересекаются, то точка пересечения делит обе проекции профильного отрезка в одном и том же соотношении.
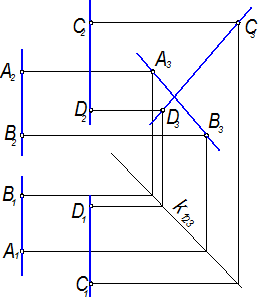 |
Рисунок 1.3.10 – Скрещивающиеся профильные прямые.
Дата добавления: 2016-06-02; просмотров: 1230;
